Counterfactual Theories of Causation
The basic idea of counterfactual theories of causation is that the meaning of causal claims can be explained in terms of counterfactual conditionals of the form “If A had not occurred, C would not have occurred”. Most counterfactual analyses have focused on claims of the form “event c caused event e”, describing ‘singular’ or ‘token’ or ‘actual’ causation. Such analyses have become popular since the development in the 1970s of possible world semantics for counterfactuals. The best-known counterfactual analysis of causation is David Lewis’s (1973b) theory. However, intense discussion over forty years has cast doubt on the adequacy of any simple analysis of singular causation in terms of counterfactuals. Recent years have seen a proliferation of different refinements of the basic idea; the ‘structural equations’ or ‘causal modelling’ framework is currently the most popular way of cashing out the relationship between causation and counterfactuals.
- 1. Lewis’s 1973 Counterfactual Analysis
- 2. Problems for Lewis’s Counterfactual Theory
- 3. Lewis’s 2000 Theory
- 4. Contextualism vs. Invariantism
- 5. The Structural Equations Framework
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. Lewis’s 1973 Counterfactual Analysis
The guiding idea behind counterfactual analyses of causation is the thought that – as David Lewis puts it – “We think of a cause as something that makes a difference, and the difference it makes must be a difference from what would have happened without it. Had it been absent, its effects – some of them, at least, and usually all – would have been absent as well” (1973b, 161).
The first explicit definition of causation in terms of counterfactuals was, surprisingly enough, given by Hume, when he wrote: “We may define a cause to be an object followed by another, and where all the objects, similar to the first, are followed by objects similar to the second. Or, in other words, where, if the first object had not been, the second never had existed” (1748, Section VII). It is difficult to understand how Hume could have confused the first, regularity definition with the second, very different counterfactual definition (though see Buckle 2004: 212–13 for a brief discussion).
At any rate, Hume never explored the alternative counterfactual approach to causation. In this, as in much else, he was followed by generations of empiricist philosophers. The chief obstacle in empiricists’ minds to explaining causation in terms of counterfactuals was the obscurity of counterfactuals themselves, owing chiefly to their reference to unactualised possibilities. The true potential of the counterfactual approach to causation did not become clear until counterfactuals became better understood through the development of possible world semantics in the early 1970s.
The best known and most thoroughly elaborated counterfactual theory of causation is David Lewis’s theory in his (1973b). Lewis’s theory was refined and extended in articles subsequently collected in his (1986a). In response to doubts about the theory’s treatment of preemption, Lewis subsequently proposed a fairly radical revision of the theory (2000/2004a). In this section we shall confine our attention to the original 1973 theory, deferring the later changes he proposed for consideration below.
- 1.1 Counterfactuals and Causal Dependence
- 1.2 The Temporal Asymmetry of Causal Dependence
- 1.3 Transitivity and Preemption
- 1.4 Chancy Causation
1.1 Counterfactuals and Causal Dependence
Like most contemporary counterfactual theories, Lewis’s theory employs a possible world semantics for counterfactuals. Such a semantics states truth conditions for counterfactuals in terms of similarity relations between possible worlds. Lewis famously espouses realism about possible worlds, according to which non-actual possible worlds are real concrete entities on a par with the actual world (Lewis 1986e). However, most contemporary philosophers would seek to deploy the explanatorily fruitful possible worlds framework while distancing themselves from full-blown realism about possible worlds themselves (see the entry on possible worlds).
The central notion of a possible world semantics for counterfactuals is a relation of comparative similarity between worlds (Lewis 1973a). One world is said to be closer to actuality than another if the first resembles the actual world more than the second does. In terms of this similarity relation, the truth condition for the counterfactual “If A were (or had been) the case, C would be (or have been) the case” is stated as follows:
- (1)
- “If A were the case, C would be the case” is true in the actual world if and only if either (i) there are no possible A-worlds; or (ii) some A-world where C holds is closer to the actual world than is any A-world where C does not hold.
We shall ignore the first case in which the counterfactual is vacuously true. The fundamental idea of this analysis is that the counterfactual “If A were the case, C would be the case” is true just in case it takes less of a departure from actuality to make the antecedent true along with the consequent than to make the antecedent true without the consequent.
In terms of counterfactuals, Lewis defines a notion of causal dependence between events, which plays a central role in his theory of causation (1973b).
- (2)
- Where c and e are two distinct possible events, e causally depends on c if and only if, if c were to occur e would occur; and if c were not to occur e would not occur.
This condition states that whether e occurs or not depends on whether c occurs or not. Where c and e are events that actually occur, this truth condition can be simplified somewhat. For in this case it follows from the second formal condition on the comparative similarity relation that the counterfactual “If c were to occur e would occur” is automatically true: this formal condition implies that a counterfactual with true antecedent and true consequent is itself true. Consequently, the truth condition for causal dependence becomes:
- (3)
- Where c and e are two distinct actual events, e causally depends on c if and only if, if c were not to occur e would not occur.
There are three important things to note about the definition of causal dependence. First, it takes the primary relata of causal dependence to be events. Lewis’s own theory of events (1986b) construes events as classes of possible spatiotemporal regions. However, different conceptions of events are compatible with the basic definition (Kim 1973a; for an alternative broadly Lewisian take on events see McDonnell 2016 and Kaiserman 2017). Indeed, it even seems possible to formulate it in terms of facts rather than events (Mellor 1995, 2004).
Second, the definition requires the causally dependent events to be distinct from each other. Distinctness means that the events are not identical, neither is part of the other, and neither implies the other. This qualification is important if spurious non-causal dependences are to be ruled out. (For this point see Kim 1973b and Lewis 1986b.) For while you would not have written ‘Larry’ if you had not written ‘rr’; and you would not have said ‘Hello’ loudly if you had not said ‘Hello’, neither dependence counts as a causal dependence since the paired events are not distinct from each other in the required sense.
Convinced by the need to make room in his analysis for causation by (and of) absence – as when the gardener’s failure to water the plants causes their death – Lewis later amended his view to the view that causal dependence is a matter of counterfactual dependence between events or their absences (Lewis 2000: §X; 2004b). We shall largely ignore this complication in what follows; for some discussion of causation by absence see Schaffer 2000b, Beebee 2004b, McGrath 2005, Livengood and Machery 2007, Dowe 2009.
Third, the counterfactuals that are employed in the analysis are to be understood according to what Lewis calls the standard interpretation. There are several possible ways of interpreting counterfactuals; and some interpretations give rise to spurious non-causal dependences between events. For example, suppose that the events c and e are effects of a common cause d. It is tempting to reason that there must be a causal dependence between c and e by engaging in the following piece of counterfactual reasoning: if c had not occurred, then d would not have occurred; and if d had not occurred, e would not have occurred. But Lewis says the former counterfactual, which he calls a backtracking counterfactual, is not to be used in the assessment of causal dependence. The right counterfactuals to be used are non-backtracking counterfactuals that typically hold the past fixed up until the time (or just before the time) at which the counterfactual’s antecedent is supposed to obtain. Thus if c had not occurred, d – which in fact occurred before c – would have occurred anyway; so on the standard interpretation, where backtracking counterfactuals are false, the inference to the claim that e causally depends on c is blocked.
1.2 The Temporal Asymmetry of Causal Dependence
What constitutes the direction of the causal relation? Why is this direction typically aligned with the temporal direction from past to future? In answer to these questions, Lewis (1979) argues that the direction of causation is the direction of causal dependence; and it is typically true that events causally depend on earlier events but not on later events. He emphasises the contingency of the latter fact because he regards backwards or time-reversed causation as a conceptual possibility that cannot be ruled out a priori. Accordingly, he dismisses any analysis of counterfactuals that would deliver the temporal asymmetry by conceptual fiat.
Lewis’s explanation of the temporal asymmetry of counterfactual dependence comes from a combination of his analysis of the similarity relation together with the (alleged) ‘asymmetry of overdetermination’ – a contingent feature of the world. According to this analysis, there are several respects of similarity to be taken into account in evaluating non-backtracking counterfactuals: similarity with respect to laws of nature and also similarity with respect to particular matters of fact. Worlds are more similar to the actual world the fewer miracles or violations of the actual laws of nature they contain. Again, worlds are more similar to the actual world the greater the spatio-temporal region of perfect match of particular fact they have with the actual world. If the laws of the actual world are deterministic, these rules will clash in assessing which counterfactual worlds are more similar to the actual world. For a world that makes a counterfactual antecedent true must differ from the actual world either in allowing some violation of the actual laws (a ‘divergence miracle’), or in differing from the actual world in particular fact. Lewis’s analysis allows a tradeoff between these competing respects of similarity in such cases. It implies that worlds with an extensive region of perfect match of particular fact can be considered very similar to the actual world provided that the match in particular facts with the actual world is achieved at the cost of a small, local miracle, but not at the cost of a big, diverse miracle.
Taken by itself, this account contains no built-in time asymmetry. That comes only when the account is combined with the asymmetry of overdetermination: the (alleged) fact that effects are rarely overdetermined by their causes, but causes are very often overdetermined by their effects. Taking an example from Elga (2000): suppose that Gretta cracks an egg at 8.00 (event c), pops it in the frying pan, and eats it for her breakfast. What would have happened had c not occurred? The right answer (Answer 1) is that the egg would not then have been fried and Gretta would not have eaten it – and not (Answer 2) that she would still have fried and eaten the egg, but these events would somehow have come about despite her failing to crack it in the first place. The question is: how does Lewis’s analysis of the similarity relation deliver Answer 1 and not Answer 2? In particular, consider worlds where there is perfect match of particular fact until just before 8.00, and then a miracle, and then no perfect match of particular fact thereafter. Call the closest such world World 1. Now consider worlds where there is no perfect match of particular fact before 8.00 (and in particular, Gretta does not crack the egg), a miracle just after 8.00, and then perfect match of particular fact thereafter. Call the closest such world World 2. (Intuitively, in the first case we keep the past fixed, insert a miracle just before 8.00 so that c doesn’t occur, and the future unfolds thereafter according to the (actual) laws. In the second case, we keep the future fixed, insert a miracle just after 8.00 so that c doesn’t occur, and the past unfolds according to the (actual) laws.) Why is World 1 closer to actuality than is World 2?
Lewis’s answer to that question comes from the fact that c leaves very many traces: at 8.02, for example, there is the egg cooking in the pan, the cracked empty shell in the bin, traces of raw egg on Gretta’s fingers, her memory of having just now cracked it, and so on. So in World 2, Gretta fails to crack the egg but then, shortly thereafter, seems to remember cracking it, there is the egg in the pan, the empty shell in the bin, and so on. So World 2 – since it contains all of these events without the egg being cracked in the first place – needs to contain not just one miracle but several: one to take care of each of these effects. World 1, by contrast, requires just the one small miracle to stop Gretta cracking the egg. Hence World 2 contains a ‘big, diverse’ miracle while World 1 contains just one small miracle; hence World 1 is closer to actuality than is World 2; hence Lewis’s analysis yields the correct result that had Gretta not cracked the egg, she would not have eaten it.
The result in Gretta’s case generalises to the extent that causes are overdetermined by their effects but effects are not overdetermined by their causes. Overdetermination of effects by causes does of course happen – as when the victim is simultaneously shot by several assassins – but it is relatively rare, and even when it happens the effect is overdetermined only by a handful of events. By contrast, the leaving of traces is ubiquitous – and (or so Lewis needs to think) the extent of overdetermination, in any given case, is much greater than in cases of cause-to-effect overdetermination. Both of these, however, are contingent features of the actual world (or so Lewis claims; but see §2.1 below).
In general, then, the symmetric analysis of similarity and the de facto asymmetry of overdetermination together imply that worlds that accommodate counterfactual changes by preserving the actual past and allowing for divergence miracles are more similar to the actual world than worlds that accommodate such changes by allowing for convergence miracles that preserve the actual future. This fact in turn implies that, where the asymmetry of overdetermination obtains, the present counterfactually depends on the past, but not on the future.
1.3 Transitivity and Preemption
As Lewis notes (1973b), causal dependence between actual events is sufficient for causation, but not necessary: it is possible to have causation without causal dependence. A standard case of ‘pre-emption’ will illustrate this. Suppose that two shooters conspire to assassinate a hated dictator, agreeing that one or other will shoot the dictator on a public occasion. Acting side by side, assassins A and B find a good vantage point, and, when the dictator appears, both take aim (events a and b respectively). A pulls her trigger and fires a shot that hits its mark, but B desists from firing when he sees A pull her trigger. Here assassin A’s actions (such as her taking aim) are causes of the dictator’s death, while B’s actions (such as his taking aim) are merely preempted potential causes. (Lewis distinguishes such cases of preemption from cases of symmetrical overdetermination in which two processes terminate in the effect, with neither process preempting the other. Lewis believes that these cases are not suitable test cases for a theory of causation since they do not elicit clear judgements.) The problem raised by this example of preemption is that both actions are on a par from the point of view of causal dependence: had neither A nor B acted, then the dictator would not have died; and if either had acted without the other, the dictator would have died.
To overcome this problem Lewis extends causal dependence to a transitive relation by taking its ancestral. He defines a causal chain as a finite sequence of actual events c, d, e, … where d causally depends on c, e on d, and so on throughout the sequence. Then causation is finally defined in these terms:
- (4)
- c is a cause of e if and only if there exists a causal chain leading from c to e.
Given the definition of causation in terms of causal chains, Lewis is able to distinguish preempting actual causes (such as a) from preempted potential causes (such as b). There is a causal chain running from a to the dictator’s death, but no such chain running from b to the dictator’s death. Take, for example, as an intermediary event occurring between a and the dictator’s death, the bullet from A’s gun speeding through the air in mid-trajectory. The speeding bullet causally depends on a, since that particular bullet would not have been in mid-trajectory had A not taken aim; and the dictator’s death causally depends on the speeding bullet, since by the time the bullet is in mid-trajectory B has refrained from firing so that the dictator would not have died without the presence of the speeding bullet. (Recall that we are not allowed to ‘backtrack’: it is not true that if the bullet had not been mid-trajectory A would not have taken aim, and hence it is not true that had the bullet not been mid-trajectory B would have fired after all.) Hence, we have a causal chain, and so causation. But no corresponding intermediary can be found between b and the dictator’s death; hence b does not count as causes of the death.
Lewis’s definition of causation also delivers the result that causation is a transitive relation: whenever c causes d and d causes e, it will also be true that c causes e. The transitivity of causation fits with at least some of our explanatory practices. For example, historians wishing to explain some significant historical event will trace the explanation back through a number of causal links, concluding that the event at the beginning of the causal chain is responsible for the event being explained. As we shall see later, however, some authors have claimed that causation is not in fact transitive.
1.4 Chancy Causation
So far we have considered how the counterfactual theory of causation works under the assumption of determinism. But what about causation when determinism fails? Lewis (1986c) argues that chancy causation is a conceptual possibility that must be accommodated by a theory of causation. Indeed, contemporary physics tells us the actual world abounds with probabilistic processes that are causal in character. To take a familiar example (Lewis 1986c): suppose that you mischievously hook up a bomb to a radioactive source and Geiger counter in such a way that the bomb explodes if the counter registers a certain number of clicks within ten minutes. If it happens that the counter registers the required number of clicks and the bomb explodes, your act caused the explosion, even though there is no deterministic connection between them: consistent with the actual past and the laws, the Geiger counter might not have registered sufficiently many clicks.
In principle a counterfactual analysis of causation is well placed to deal with chancy causation, since counterfactual dependence does not require that the cause was sufficient, in the circumstances, for the effect – it only requires that the cause was necessary in the circumstances for the effect. The problem posed by abandoning the assumption of determinism, however, is that pervasive indeterminism undermines the plausibility of the idea that – preemption and overdetermination aside – effects generally counterfactually depend on their causes. In the Geiger counter case above, for example, suppose that the chance of the bomb exploding can be altered by means of a dial. (A low setting means the Geiger counter needs to register a lot of clicks in order for the bomb to go off in the next ten minutes, thus making the explosion very unlikely; a high setting means it needs to register very few clicks, thus making the explosion very likely.) The dial is on a low setting; I increase the chance of the bomb exploding by turning it up. My act was a cause of the explosion, but it’s not true that, had I not done it, the bomb would not have exploded; it would merely have been very unlikely to do so.
In order to accommodate chancy causation, Lewis (1986c) defines a more general notion of causal dependence in terms of chancy counterfactuals. These counterfactuals are of the form “If A were the case Pr (C) would be x”, where the counterfactual is an ordinary would-counterfactual, interpreted according to the semantics above, and the Pr operator is a probability operator with narrow scope confined to the consequent of the counterfactual. Lewis interprets the probabilities involved as temporally indexed single-case chances. (See his (1980) for the theory of single-case chance.)
The more general notion of causal dependence reads:
- (5)
- Where c and e are distinct actual events, e causally depends on c if and only if, if c had not occurred, the chance of e’s occurring would be much less than its actual chance.
This definition covers cases of deterministic causation in which the chance of the effect with the cause is 1 and the chance of the effect without the cause is 0. But it also allows for cases of irreducible probabilistic causation where these chances can take non-extreme values, as in the Geiger-counter-with-dial example above. It is similar to the central notion of probabilistic relevance used in probabilistic theories of type-causation, except that it employs chancy counterfactuals rather than conditional probabilities. (See the discussion in Lewis 1986c for the advantages of the counterfactual approach over the probabilistic one. Also see the entry probabilistic causation.)
The rest of the theory of chancy causation follows the outlines of the theory of deterministic causation: again, we have causation when we have one or more steps of causal dependence.
2. Problems for Lewis’s Counterfactual Theory
In this section we consider the principal difficulties for Lewis’s theory that have emerged in discussion over the last forty-five years.
2.1 Temporal Asymmetry
There have been several important critical discussions of Lewis’s explanation of the temporal asymmetry of causation. (For some early discussions see Horwich 1987: Chap. 10; Hausman 1998: Chap. 6; Price 1996: Chap. 6.) One important criticism concerns the ‘asymmetry of miracles’ that is central to Lewis’s account of the temporal asymmetry of causation: a miracle that realises a counterfactual antecedent about particular facts at time t by having a possible world diverge from the actual world just before the time t is, Lewis claims, smaller and less diverse than a miracle that realises the same counterfactual antecedent and makes a possible world converge to the actual world after the time t. Adam Elga (2000) has argued that the asymmetry of miracles does not hold in many cases.
Elga’s argument proceeds by way of the example of Gretta cracking an egg described earlier, and the basic idea is that in fact World 2 above – the closest world where particular fact in the past up until shortly after 8.00 doesn’t match actuality (and, in particular, Gretta doesn’t crack the egg), there is a miracle shortly after 8.00, and thereafter World 2 evolves according to the actual world’s laws and matches actuality perfectly with respect to particular fact. Thinking in the future-to-past direction for now, consider what happens at the actual world from a time-reversed point of view: Gretta transfers the egg from her plate to the hot pan, the pan cools down and the egg uncooks, and then it leaps up into the waiting shell, which closes neatly around it. Now (to get us to World 2) insert a small miracle – at 8.05, say, when the egg is nicely cooked in the pan – altering just the positions of a few molecules, say, so that what happens (again, proceeding from future to past) is that (lawfully, once the miracle has occurred) the egg just sits in the pan, cooling down and transferring heat to the pan in the process, and then gradually rots in the way that eggs normally do (except that they normally do that in the past-to-future direction). The idea is that, while World 2 (viewed from past to future) looks exceedingly strange – after all, it involves Gretta devouring what was once a horrible rotten egg that somehow found its way into her pan and then bizarrely de-rotted – none of that is unlawful. It is just, thanks to the laws of thermodynamics, spectacularly unlikely.
But how does this help us with the original problem with World 2, namely the fact that all of the traces of Gretta’s actual egg-cracking, such as her remembering cracking it, the presence of the empty, broken eggshell in the bin, and so on, would have to somehow be individually be brought about in World 2 by additional miracles, in order to preserve perfect match of particular fact from 8.05 onwards? The short answer is that they don’t. The ‘traces’ are there in World 2 all right, and of course we would normally expect such ‘traces’ to point pretty conclusively to Gretta having recently cracked an egg. But they don’t lawfully entail that she did. Again looking at World 2 from a time-reversed perspective, we take the world as it is after 8.05, ‘traces’ and all, and run the laws backwards (apart from the small miracle that makes the egg rot slowly in the pan rather than leaping up into the waiting shell). What ‘follows’ (still going backwards in time) is anyone’s guess, and whatever it is it will doubtless look bizarre when viewed in the usual, past-to-future direction. Be that as it may, World 2 is a world with a single, small miracle at 8.05, with perfect match of particular fact thereafter, which is just as close to the actual world as is World 1, where there is a small miracle before Gretta cracks the egg. So, Elga argues, there is no asymmetry of counterfactual dependence, as Lewis defines it.
Several authors have come to the conclusion that a viable account of the asymmetry of counterfactual dependence must derive not from the asymmetry of miracles, as Lewis claims, but from thermodynamic asymmetry: from the fact that entropy increases towards the future. In particular, David Albert (2000) proposes that we need to assume the ‘Past Hypothesis’: the assumption that the universe began in an extremely low entropy condition. The Past Hypothesis and its relationship to the asymmetry of counterfactual dependence has been much discussed. (See Frisch 2005, 2007; Loewer 2007; Price and Weslake 2009; Kutach 2002, 2013.)
2.2 Transitivity
As we have seen, Lewis builds transitivity into causation by defining causation in terms of chains of causal dependence. However, a number of alleged counter-examples have been presented which cast doubt on transitivity. (Lewis 2004a presents a short catalogue of these counterexamples.) Here is a sample of two counterexamples.
First, an unpublished but much-discussed example due to Ned Hall. A hiker is walking along a mountain trail, when a boulder high above is dislodged and comes careering down the mountain slopes. The hiker notices the boulder and ducks at the appropriate time. The careering boulder causes the hiker to duck and this, in turn, causes his continued stride. (This second causal link involves double prevention: the duck prevents the collision between hiker and boulder which, had it occurred, would have prevented the hiker’s continued stride.) However, the careering boulder is the sort of thing that would normally prevent the hiker’s continued stride and so it seems counterintuitive to say that it causes the stride.
Second, an example due to Douglas Ehring (1987). Jones puts some potassium salts into a hot fire. Because potassium compounds produce a purple flame when heated, the flame changes to a purple colour, though everything else remains the same. The purple flame ignites some flammable material nearby. Here we judge that putting the potassium salts in the fire caused the purple flame, which in turn caused the flammable material to ignite. But it seems implausible to judge that putting the potassium salts in the fire caused the flammable material to ignite.
Various replies have been made to these counterexamples. L.A. Paul (2004) offers a response to the second example that involves conceiving of the relata of causation as event aspects: she argues that there is mismatch between the event aspect that is the effect of the first causal link (the flame’s being a purple colour) and the event aspect that is the cause of the second causal link (the flame’s touching the flammable material). Thus, while it’s true that the purple flame did not cause the ignition, there is no failure of transitivity after all. Maslen (2004) solves the problem by appealing to a contrastivist account of causation (see §4 below): the contrast situation at the effect-end of the first causal statement does not match up with the contrast situation at the cause-end of the second causal statement. Thus, the first causal statement should be interpreted as saying that Jones’s putting potassium salts in the fire rather not doing so caused the flame to turn purple rather than yellow; but the second causal statement should be interpreted as saying that the purple fire’s occurring rather than not occurring caused the flammable material to ignite rather not to ignite. Where there is a mismatch of this kind, we do not have a genuine counterexample to transitivity.
The first example cannot be handled in the same way. Some defenders of transitivity have replied that our intuitions about the intransitivity of causation in these examples are misleading. For instance, Lewis (2004a) points out that the counterexamples to transitivity typically involve a structure in which a c-type event generally prevents an e-type but in the particular case the c-event actually causes another event that counters the threat and causes the e-event. If we mix up questions of what is generally conducive to what, with questions about what caused what in this particular case, he says, we may think that it is reasonable to deny that c causes e. But if we keep the focus sharply on the particular case, we must insist that c does in fact cause e.
The debate about the transitivity of causation is not easily settled, partly because it is tied up with the issue of how it is best for a counterfactual theory to deal with examples of preemption. As we have seen, Lewis’s counterfactual theory relies on the transitivity of causation to handle cases of preemption. If such cases could be handled in some other way, that would take some of the theoretical pressure off the theory, allowing it to concede the alleged counterexamples to transitivity without succumbing to the difficulties posed by preemption. (For more on this point see Hitchcock 2001. For an extensive discussion of the issues around transitivity see Paul and Hall 2013: Chap. 5.)
2.3 Preemption
As we have seen, Lewis employs his strategy of defining causation in terms of chains of causal dependence not only to make causation transitive, but also to deal with preemption examples. However, there are preemption examples that this strategy cannot deal with satisfactorily. Difficulties concerning preemption have proven to be the biggest bugbear for Lewis’s theory. (Paul and Hall 2013: Chap. 3 contains an extensive discussion of the problems posed by preemption and other kinds of redundant causation for counterfactual theories.)
In his (1986c: 200), Lewis distinguishes cases of early and late preemption. In early preemption examples, the process running from the preempted alternative is cut short before the main process running from the preempting cause has gone to completion. The example of the two assassins, given above, is an example of this sort. The theory of causation in terms of chains of causal dependence can handle this sort of example. In contrast, cases of late preemption are ones in which the process running from the preempted cause is cut short by the main process running to completion and bringing about the effect before the preempted potential cause has the opportunity to do so. The following is an example of late preemption due to Hall (2004).
Billy and Suzy throw rocks at a bottle. Suzy throws first so that her rock arrives first and shatters the glass; Billy’s rock sails through the air where the bottle had stood moments earlier. Without Suzy’s throw, Billy’s throw would have shattered the bottle. However, Suzy’s throw caused the bottle to shatter, while Billy’s throw is merely a preempted potential cause. This is a case of late preemption because the alternative process (Billy’s throw) is cut short by the main process (Suzy’s throw) running to completion.
Lewis’s theory cannot explain the judgement that Suzy’s throw caused the shattering of the bottle. For there is no causal dependence between Suzy’s throw and the shattering, since even if Suzy had not thrown her rock, the bottle would have shattered due to Billy’s throw. Nor is there a chain of stepwise dependences running cause to effect, because there is no event intermediate between Suzy’s throw and the shattering that links them up into a chain of dependences. Take, for instance, Suzy’s rock in mid-trajectory. This event depends on Suzy’s initial throw, but the problem is that the shattering of the bottle does not depend on it, because even without it the bottle would still have shattered because of Billy’s throw.
To be sure, the bottle shattering that would have occurred without Suzy’s throw would be different from the bottle shattering that actually occurred with Suzy’s throw. For a start, it would have occurred later. This observation suggests that one solution to the problem of late preemption might be to insist that the events involved should be construed as fragile events. Accordingly, it will be true rather than false that if Suzy had not thrown her rock, then the actual bottle shattering, taken as a fragile event with an essential time and manner of occurrence, would not have occurred. Lewis himself does not endorse this response on the grounds that a uniform policy of construing events as fragile would go against our usual practices, and would generate many spurious causal dependences. For example, suppose that a poison kills its victim more slowly and painfully when taken on a full stomach. Then the victim’s eating dinner before he drinks the poison would count as a cause of his death since the time and manner of the death depend on the eating of the dinner. (For discussion of the limitations of this response see Lewis 1986c, 2000.)
The solution to the late preemption problem that Lewis cautiously endorses in his 1986c appeals to the notion of quasi-dependence. Consider a case that resembles the case of Billy and Suzy throwing rocks at a bottle. Suzy throws a rock (c) and shatters the bottle (e) in exactly the same way in which she does in the original case. But in this case Billy and his rock are entirely absent. In the original case, e is caused by but does not counterfactually depend on c, whereas in this second case e is caused by and does counterfactually depend on c. But the intrinsic character of the process leading from c to e is just the same in both cases. Thus, Lewis says, in the original case (with Billy also throwing), e quasi-depends on c. So “we could redefine a causal chain as a sequence of two or more events, with either dependence or quasi-dependence at each step. And as always, one event is a cause of another iff there is a causal chain from one to the other” (1986c, 206). (A related idea is pursued in Menzies 1996 and 1999.) Note that, this proposed definition of a causal chain notwithstanding, the quasi-dependence solution does not demand transitivity in the way that Lewis’s earlier solution to the problem of early preemption did: with back-up potential causes safely out of the way, in all cases of preemption (early and late), the effect should straightforwardly quasi-depend on its cause.
Lewis’s dissatisfaction with his own attempts to deal with the problem of late preemption, as well as his theory’s inability to deal with ‘trumping preemption’ (Schaffer 2000a), led to the development of his 2000 theory. A further problem relating to preemption that arises for chancy causation – which the 2000 theory does not address – is discussed in §5.4 below.
3. Lewis’s 2000 Theory
In an attempt to deal with the various problems facing his 1973 theory, Lewis developed a new version of the counterfactual theory, which he first presented in his Whitehead Lectures at Harvard University in March 1999. (A shortened version of the lectures appeared as his 2000. The full lectures are published as his 2004a.)
Counterfactuals play a central role in the new theory, as in the old. But the counterfactuals it employs do not simply state dependences of whether one event occurs on whether another event occurs. The counterfactuals state dependences of whether, when, and how one event occurs on whether, when, and how another event occurs. A key idea in the formulation of these counterfactuals is that of an alteration of an event. This is an actualised or unactualised event that occurs at a slightly different time or in a slightly different manner from the given event. An alteration is, by definition, a very fragile event that could not occur at a different time, or in a different manner without being a different event. Lewis intends the terminology to be neutral on the issue of whether an alteration of an event is a version of the same event or a numerically different event.
The central notion of the new theory is that of influence:
- (6)
- Where c and e are distinct events, c influences e if and only if there is a substantial range c1, c2, … of different not-too-distant alterations of c (including the actual alteration of c) and there is a range e1, e2, … of alterations of e, at least some of which differ, such that if c1 had occurred, e1 would have occurred, and if c2 had occurred, e2 would have occurred, and so on.
Where one event influences another, there is a pattern of counterfactual dependence of whether, when, and how upon whether, when, and how. As before, causation is defined as an ancestral relation:
- (7)
- c causes e if and only if there is a chain of stepwise influence from c to e.
One of the points Lewis advances in favour of this new theory is that it handles cases of late as well as early preemption. (The theory is restricted to deterministic causation and so does not address the example of probabilistic preemption described below in §5.4.) Reconsider, for instance, the example of late preemption involving Billy and Suzy throwing rocks at a bottle. The theory is supposed to explain why Suzy’s throw, and not Billy’s throw, is the cause of the shattering of the bottle. If we take an alteration in which Suzy’s throw is slightly different (the rock is lighter, or she throws sooner), while holding fixed Billy’s throw, we find that the shattering is different too. But if we make similar alterations to Billy’s throw while holding Suzy’s throw fixed, we find that the shattering is unchanged.
Another point in favour of the new theory is that it handles cases of ‘trumping’ preemption, first described by Jonathan Schaffer (2000a). Lewis gives an example involving a major and a sergeant who are shouting orders at the soldiers. The major and sergeant simultaneously shout ‘Advance!’; the soldiers hear them both and advance. Since the soldiers obey the superior officer, they advance because the major orders them to, not because the sergeant does. So the major’s command preempts or trumps the sergeant’s. Other theories have difficulty with trumping cases, including – or so Lewis believes – his own attempt to solve the late preemption problem by appealing to quasi-dependence (2000, 184-5). The trumping case is one in which the causal chain leading from the sergeant’s shout to the soldiers’ advancing runs to completion – or at least, Lewis thinks, it is epistemically possible that it does – just as the chain leading from the major’s shouting does. So it is an intrinsic duplicate of the comparison case where the sergeant shouts but the major doesn’t; hence the soldiers’ advancing quasi-depends on the sergeant’s shout, which is the wrong result. Lewis’s argues that his new theory handles trumping cases with ease. Altering the major’s command while holding fixed the sergeant’s, the soldier’s response would be correspondingly altered. In contrast, altering the sergeant’s command, while holding fixed the major’s, would make no difference at all.
There is, however, some reason for scepticism about whether the new theory handles the examples of late preemption and trumping completely satisfactorily. In the example of late preemption, Billy’s throw has some degree of influence on the shattering of the bottle. For if Billy had thrown his rock earlier (so that it preceded Suzy’s throw) and in a different manner, the bottle would have shattered earlier and in a different manner. Likewise, the sergeant’s command has some degree of influence on the soldiers’ advance in that if the sergeant had shouted earlier than the major with a different command, the soldiers would have obeyed his order. In response to these points, Lewis must say that these alterations of the events are too distant to be considered relevant. But some metric of distance in alterations is required, since it seems that similar alterations of Suzy’s throw and the major’s command are relevant to their having causal influence.
It has also been argued that the new theory generates a great number of spurious cases of causation (Collins 2000; Kvart 2001). The theory implies that any event that influences another event to a certain degree counts as one of its causes. But common sense is more discriminating about causes. To take an example of Jonathan Bennett (1987): rain in December delays a forest fire; if there had been no December rain, the forest would have caught fire in January rather than when it actually did in February. The rain influences the fire with respect to its timing, location, rapidity, and so forth. But common sense denies that the rain was a cause of the fire, though it allows that it is a cause of the delay in the fire. Similarly, in the example of the poison victim discussed above, the victim’s ingesting poison on a full stomach influences the time and manner of his death (making it a slow and painful death), but common sense refuses to countenance his eating dinner as a cause of his death, though it may countenance it as a cause of its being a slow and painful death. Pace Lewis, common sense does not take just anything that affects the time and manner of an event to be a cause of the event simpliciter.
4. Contextualism vs. Invariantism
A question that has received increasing attention in recent years is whether causation is an ‘invariant’ relation or whether, instead, the truth of a given causal claim varies according to the context within which it is under discussion. (Note that ‘invariant’ is often used to describe a causal relationship that is stable across a wide range of different circumstances; this is not the meaning of ‘invariant’ as it is being used here.) There is a wealth of evidence that people’s causal judgements are sensitive to contextual factors (Hilton & Slugoski 1986; Cheng & Novick 1991; Knobe & Fraser 2008; Hitchcock & Knobe 2009; Clarke et al. 2015; Kominsky et al. 2015; Icard et al. 2017); however, in principle one might hold the invariantist line and insist that what varies with context is not truth but merely assertibility.
Consider a standard problem case: the gardener and the Queen equally fail to water my flowers while I’m on holiday, and their subsequent death (e) counterfactually depends equally on their omissions. But many people’s judgement is that only the gardener’s – and not the Queen’s – omission is a genuine cause of their death (Beebee 2004b, McGrath 2005, Livengood & Machery 2007). We might accommodate that judgement by claiming that it is false that the Queen’s omission was a cause of e, and conclude that we need some additional constraint on causation aside from counterfactual dependence, e.g. that causes must be ‘deviant’ or abnormal: the gardener’s behaviour was deviant (he was supposed to, or perhaps normally does, water my flowers) but the Queen’s was entirely normal (she never waters my flowers, nor would anyone expect her to). Or we might accommodate the judgement by appealing to pragmatic factors such as salience: the gardener’s and the Queen’s omissions are both, equally, causes of e, but in most conversational contexts the Queen’s omission simply isn’t relevant. For example, if I’m interested in finding out who is to blame for the flowers’ death, the Queen’s neglect is simply irrelevant to my investigation since it’s obvious that she is not to blame.
Lewis himself takes this latter, invariantist approach (Lewis 2004b). The causes of any given event are many and varied, and in any given explanatory context most of them fail to be salient; that is why it strikes us as wrong to mention them (Lewis 1986d). Lewis’s approach is to explain (some of) the phenomena that motivate contextualism by appealing to a broadly Gricean story about conversational implicature. An advantage of invariantism is that it allows us to conceive of causation as a fully objective, mind-independent – or, as Menzies (2009: 342) puts it, a ‘natural’ – relation.
It is unclear, however, that all alleged cases of context-dependence can be dealt with in this manner. Suzy’s theft of the coconut cake from the shop caused her subsequent illness: having bought the cake, she ate it – but (as she soon discovered) she’s allergic to coconut. Or did it? It depends, it would seem, on what we contrast her theft of the coconut cake with. If she’d left the shop empty-handed – or stolen a Bath bun instead – she wouldn’t have been ill. But if she’d paid for the cake instead of stealing it, she still would have been ill. We sometimes mark the intended contrast by, for example, stress: Suzy’s theft of the coconut cake caused her illness, but her theft of the coconut cake didn’t.
Lewis’s original theory of events (1986b) was tailor-made to deal with such cases – or so it might seem. According to that theory, an event is a set of spatio-temporal regions of worlds. We can distinguish between, for example, the event that is essentially Suzy’s theft of a cake (e1) and the event that is essentially her acquiring (one way or another) a coconut cake (e2): the two events consist in two different (but overlapping) sets of spatio-temporal regions of worlds that share their actual-world member, namely what actually happened in the cake shop. And so – at least on the face of it – we can say that e2 was a cause of her illness but e1 was not (since had she not stolen a cake, she would have bought the coconut cake instead).
It is unclear, however, that appeal to the essential features of events successfully deals with the problem. After all, what if, had Suzy not stolen a cake, the cake she would have bought was a Bath bun and not the coconut cake she actually stole? (She really wanted a cake but didn’t have enough money for the coconut cake.) And in any case, Lewis’s own official view is that in supposing a putative cause c absent we ‘imagine that c is completely and cleanly excised from history, leaving behind no fragment or approximation of itself’ (2004a: 90). So we don’t appear to be able to recover the truth of the claim that Suzy’s theft of the cake was not a cause of her subsequent illness. Moreover, Lewis’s 2000 theory of causation as influence abandons the distinction between the essences of events to which the above response appealed: we have various alterations of the theft of the coconut cake (c) – including the purchase of a coconut cake and the theft of a Bath bun, for example – some of which would have resulted in an alteration of the effect e (Suzy’s illness) and some of which would not have. The degree of influence of c on e either is or is not sufficient to make it the case that c was a cause of e; either way, ‘Suzy’s theft of the coconut cake was a cause of her illness’ comes out either true or false independently of context, which – according to the contextualist – is the wrong result. (The invariantist, however, might insist that there is no real problem here. ‘Because she stole a coconut cake’ would be an inappropriate response to the question ‘Why is Suzy ill?’ if the request comes from the doctor, who is not interested in how she procured the cake; but it would be an appropriate response in the context of a discussion about, say, Suzy getting her comeuppance from her shoplifting habit.)
Cei Maslen (2004), Jonathan Schaffer (2005) and Robert Northcott (2008) all defend ‘contrastive’ accounts of causation. Schaffer conceives causation as a four-place relation – c rather than c* caused e rather than e* – and claims that context (or other devices, such as stress on a particular word) generally fixes the implied contrasts (c* and e*) in our ordinary, two-place causal talk, thereby playing a role in the truth or falsity of our (two-place) causal claims. Note that contrastivism about causation is a distinct position from the view that explanations are (always or sometimes) contrastive (see e.g. Lewis 1986d, §VI; Lipton 1991; Hitchcock 1999). On a contrastivist view of explanation, explanations (always or sometimes) take the form ‘Why P rather than Q?’, where the contrast (Q) may be explicitly stated or implied by the context in which the question ‘Why P?’ is asked. Such a view is entirely compatible with an invariantist view of causation, since the role of the contrast may merely be to select which of P’s causes is cited appropriately in answering the question. Note also that contrastivism about explanation does not appear to solve the (alleged) problem at hand. In the case of Suzy’s theft of the cake, it is the contrast on the side of causes (and hence explananda) that is at issue, and not the contrast on the side of the effect (explanandum); it is unclear how we might vary the contextually salient contrast to ‘Suzy became ill’ in such a way that different contrasts deliver different verdicts on whether ‘Suzy stole the coconut cake’ is an appropriate explanans.
While the contrastivist account of causation is generally considered to be a version of causal contextualism, contrastivism is nonetheless invariantist in the sense that there is a context-independent fact of the matter about which four-place causal relations hold: it’s just plain true that Suzy’s stealing the cake rather than leaving empty-handed caused her to be ill rather than well, and false that her stealing rather than buying the cake caused her to be ill rather than well. The contrastivist account might therefore be seen as a kind of middle road between invariantism and contextualism. (See Steglich-Petersen 2012 and Montminy & Russo 2016 for critical discussions of contextualism/contrastivism.)
The contextualist/invariantist debate arises in a slightly different form in much of the debate about the structural equations framework (see §5.5 below), to which we now turn.
5. The Structural Equations Framework
A number of contemporary philosophers have explored an alternative counterfactual approach to causation that employs the structural equations framework. (Early exponents include Hitchcock 2001, 2007; Woodward 2003; Woodward and Hitchcock 2003.) This framework, which has been used in the social sciences and biomedical sciences since the 1930s and 1940s, received its state-of-the-art formulation in Judea Pearl’s landmark 2000 book. Hitchcock and Woodward acknowledge their debt to Pearl’s work and to related work on causal Bayes nets by Peter Spirtes, Clark Glymour, and Richard Scheines (2001). However, while Pearl and Spirtes, Glymour and Scheines focus on issues to do with causal discovery and inference, Woodward and Hitchcock focus on issues of the meaning of causal claims. For this reason, their formulations of the structural equations framework are better suited to the purposes of this discussion. The exposition of this section largely follows that of Hitchcock 2001.
5.1 SEF: The Basic Picture
The structural equations framework describes the causal structure of a system in terms of a causal model of the system, which is identified as an ordered pair <V, E>, where V is a set of variables and E a set of structural equations stating deterministic relations among the variables. (We shall confine our attention to deterministic systems here; see §5.4 for a brief discussion of chancy causation.) The variables in V describe the different possible states of the system in question. While they can take any number of values, in the simple examples to be considered here the variables are binary variables that take the value 1 if some event occurs and the value 0 if the event does not occur. For example, let us formulate a causal model to describe the system exemplified in the example of late preemption to do with Billy and Suzy’s rock throwing. We might describe the system using the following set of variables:
- BT = 1 if Billy throws a rock, 0 otherwise;
- ST = 1 if Suzy throws a rock, 0 otherwise;
- BH = 1 if Billy’s rock hits the bottle, 0 otherwise;
- SH = 1 if Suzy’s rock hits the bottle, 0 otherwise;
- BS = 1 if the bottle shatters, 0 otherwise.
Here the variables are binary. But a different model might have used many-valued variables to represent the different ways in which Billy and Suzy threw their rocks, their rocks hit the bottle, or the bottle shattered.
The structural equations in a model specify which variables are to be held fixed at their actual values and how the values of other variables depend on one another. There is a structural equation for each variable. The form taken by a structural equation for a variable depends on which kind of variable it is. The structural equation for an exogenous variable (the values of which are determined by factors outside of the model) takes the form of Z = z, which simply states the actual value of the variable. The structural equation for an endogenous variable (the values of which are determined by factors within the model) states how the value of the variable is determined by the values of the other variables. It takes the form:
Y = f(X1,…, Xn)
What does this structural equation mean? There are in fact competing interpretations. Pearl (2000) regards the structural equations as the conceptual primitives of his framework, describing them as representing ‘the basic mechanisms’ of the system under investigation. However, for the purposes of exposition, it is more convenient to follow the interpretation of Woodward (2003) and Hitchcock (2001), who think of the structural equations as expressing certain basic counterfactuals of the following form:
If it were the case that X1 = x1, X2 = x2,…, Xn = xn, then it would be the case that Y = f(x1,…,xn).
As this form of counterfactual suggests, the structural equations are to be read from right to left: the antecedent of the counterfactual states possible values of the variables X1 through to Xn and the consequent states the corresponding value of the endogenous variable Y. There is a counterfactual of this kind for every combination of possible values of the variables X1 through to Xn. It is important to note that a structural equation of this kind is therefore not, strictly speaking, an identity since there is a right-to-left asymmetry built into it. This asymmetry corresponds to the asymmetry of non-backtracking counterfactuals. For example, supposing that the actual situation is one in which neither Suzy nor Billy throws a rock so the bottle does not shatter, the non-backtracking counterfactual “If either Suzy or Billy had thrown a rock, the bottle would have shattered” is true. But the counterfactual “If the bottle had shattered, either Suzy or Billy would have thrown a rock” is false.
As an illustration, consider the set of structural equations that might be used to model the late preemption example of Billy and Suzy. Given the set of variables V listed above, the members of the set of the structural equations E might be stated as follows:
- ST = 1;
- BT = 1;
- SH = ST;
- BH = BT & ~SH;
- BS = SH v BH.
In these equations logical symbols are used to represent mathematical functions on binary variables: ~X = 1 − X; X v Y = max{X, Y}; X & Y = min{X, Y}. The first two equations simply state the actual values of the exogenous variables ST and BT. The third equation encodes two counterfactuals, one for each possible value of ST. It states that if Suzy had thrown a rock (which in fact she did), her rock would have hit the bottle; and if she hadn’t thrown a rock, it wouldn’t have hit the bottle. The fourth equation encodes four counterfactuals, one for each possible combination of values for BT and ~SH. It states that if Billy had thrown a rock and Suzy’s rock hadn’t hit the bottle, Billy’s rock would have hit the bottle, but it wouldn’t have done so if one or more of these conditions had not been met. The fifth equation also encodes four counterfactuals, one for each possible combination of values for SH and BH. It states that if one or other (or possibly both) of Suzy’s rock or Billy’s rock had hit the bottle, the bottle would have shattered; but if neither rock had hit the bottle, the bottle wouldn’t have shattered.
The structural equations above can be represented in terms of a directed graph. The variables in the set V are represented as nodes in the graph. An arrow directed from one node X to another Y represents the fact that the variable X appears on the right-hand side of the structural equation for Y. In this case, X is said to be a parent of Y. Exogenous variables are represented by nodes that have no arrows directed towards them. A directed path from X to Y in a graph is a sequence of arrows that connect X with Y. The directed graph of the model described above of Billy and Suzy example is depicted in Figure 1 below:
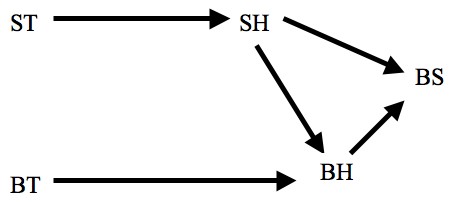
Figure 1.
The arrows in this figure tell us that the bottle’s shattering is a function of Suzy’s rock hitting the bottle and Billy’s rock hitting the bottle; that Billy’s rock hitting the bottle is a function of Billy’s throwing a rock and Suzy’s rock hitting the bottle; and that Suzy’s rock hitting the bottle is a function of her throwing the rock. It’s important to note that the nodes in the graph represent variables and not – as in the case of ‘neuron diagrams’, such as those found in Lewis 1986c – values of variables. Note also that while the arrows tell us that there are counterfactual dependence relations between the values of the variables – all of the possible values, not just the actual ones – they don’t tells us what those dependence relations are; for that, you have to look at the structural equations. For example, the directed graph only tells us that the value of BH counterfactually depends somehow or other on the values of BT and SH; e.g. it doesn’t tell us that if Billy had thrown and Suzy’s rock hadn’t hit, Billy’s rock would have hit.)
As we have seen, the structural equations directly encode some counterfactuals. However, some counterfactuals that are not directly encoded can be derived from them. Consider, for example, the counterfactual “If Suzy’s rock had not hit the bottle, it would still have shattered”. As a matter of fact, Suzy’s rock did hit the bottle. But we can determine what would have happened if it hadn’t done so, by replacing the structural equation for the endogenous variable SH with the equation SH = 0, keeping all the other equations unchanged. So, instead of having its value determined in the ordinary way by the variable ST, the value of SH is set ‘miraculously’. Pearl describes this as a ‘surgical intervention’ that changes the value of the variable. In terms of its graphical representation, this amounts to wiping out the arrow from the variable ST to the variable SH and treating SH as if it were an exogenous variable. After this operation, the value of the variable BS can be computed and shown to be equal to 1: given that Billy had thrown his rock, his rock would have hit the bottle and shattered it. So this particular counterfactual is true. This procedure for evaluating counterfactuals has direct affinities with Lewis’s non-backtracking interpretation of counterfactuals: the surgical intervention that sets the variable SH at its hypothetical value but keeps all other equations unchanged is similar in its effects to Lewis’s small miracle that realises the counterfactual antecedent but preserves the past.
In general, to evaluate a counterfactual, say “If it were the case that X1,…,Xn, then …”, one replaces the original equation for each variable Xi with a new equation stipulating its hypothetical value,while keeping the other equations unchanged; then one computes the values for the remaining variables to see whether they make the consequent true. This technique of replacing an equation with a hypothetical value set by a ’surgical intervention’ enables us to capture the notion of counterfactual dependence between variables:
- (8)
- A variable Y counterfactually depends on a variable X in a model if and only if it is actually the case that X = x and Y = y and there exist values x′ ≠ x and y′ ≠ y such that replacing the equation for X with X = x′ yields Y = y′.
Of course, so far we just have something we are calling a ‘causal model’, ⟨V, E⟩; we haven’t been told anything about how to extract causal information from it. As should be obvious by now, the basic recipe is going to be roughly as follows: the truth of ‘c causes e’ (or ‘c is an actual cause of e’), where c and e are particular, token events, will be a matter of the counterfactual relationship, as encoded by the model, between two variables X and Y, where the occurrence of c is represented by a structural equation of the form X = x1 and the occurrence of e is represented by a structural equation of the form Y = y1. We can see straightaway, however, that we can’t straightforwardly identify causation with counterfactual dependence as defined in (8) above. That would get us the truth of “Suzy’s throw caused her rock to hit the bottle” (ST = 1 and SH = 1, and, since SH = ST is a member of E, we know that if we replace ST = 1 with ST = 0, we get SH = 0). But it won’t get us, for example, the truth of “Suzy’s throw caused the bottle to shatter”, since if we replace ST = 1 with ST = 0 and work through the equations we still end up with BS = 1.
How, then, might we define ‘actual causation’ using the structural equations framework? We’ll get there by considering how SEF deals with cases of late preemption such as the Suzy and Billy case. Halpern and Pearl (2001, 2005), Hitchcock (2001), and Woodward (2003) all give roughly the same treatment of late preemption. The key to their treatment is the employment of a certain procedure for testing the existence of a causal relation. The procedure is to look for an intrinsic process connecting the putative cause and effect; suppress the influence of their non-intrinsic surroundings by ‘freezing’ those surroundings as they actually are; and then subject the putative cause to a counterfactual test. So, for example, to test whether Suzy’s throwing a rock caused the bottle to shatter, we should examine the process running from ST through SH to BS; hold fix at its actual value (that is, 0) the variable BH which is extrinsic to this process; and then wiggle the variable ST to see if it changes the value of BS. The last steps involve evaluating the counterfactual “If Suzy hadn’t thrown a rock and Billy’s rock hadn’t hit the bottle, the bottle would not have shattered”. It is easy to see that this counterfactual is true. In contrast, when we carry out a similar procedure to test whether Billy’s throwing a rock caused the bottle to shatter,we are required to consider the counterfactual “If Billy hadn’t thrown his rock and Suzy’s rock had hit the bottle, the bottle would not shattered”. This counterfactual is false. It is the difference in the truth-values of these two counterfactuals that explains the fact that it was Suzy’s rock throwing, and not Billy’s, that caused the bottle to shatter. (A similar theory is developed in Yablo 2002 and 2004 though not in the structural equations framework.)
Hitchcock (2001) presents a useful regimentation of this reasoning. He defines a route between two variables X and Z in the set V to be an ordered sequence of variables <X, Y1,…, Yn, Z> such that each variable in the sequence is in V and is a parent of its successor in the sequence. A variable Y (distinct from X and Z) is intermediate between X and Z if and only if it belongs to some route between X and Z. Then he introduces the new concept of an active causal route:
- (9)
- The route <X, Y1,…, Yn, Z> is active in the causal model <V, E> if and only if Z depends counterfactually on X within the new system of equations E’ constructed from E as follows: for all Y in V, if Y is intermediate between X and Z but does not belong to the route <X, Y1,…, Yn, Z>, then replace the equation for Y with a new equation that sets Y equal to its actual value in E. (If there are no intermediate variables that do not belong to this route, then E’ is just E.) (Hitchcock 2001: 286).
This definition generalises the informal idea sketched in the example of Suzy and Billy. <ST, SH, BS> is an active causal route because when we hold BH fixed at its actual value (Billy’s rock doesn’t hit the bottle), BS counterfactually depends on ST. By contrast, the route <BT, BH, BS> is not active because when we hold SH fixed at its actual value (Suzy’s rock does hit the bottle), BS does not counterfactually depend on BT.
In terms of the notion of an active causal route, Hitchcock defines actual or token causation in the following terms:
- (10)
- If c and e are distinct actual events and X and Z are binary variables whose values represent the occurrence and non-occurrence of these events, then c is a cause of e if and only if there is an active causal route from X to Z in an appropriate causal model <V, E>.
(We shall return to the notion of an ‘appropriate causal model’ in §5.3 below.)
As stated, (10) doesn’t handle cases of symmetric overdetermination – as when Suzy and Billy both throw their rocks independently, each throw is sufficient for the bottle to break, and both rocks hit the bottle – so neither throw preempts the other, since neither throw is on an active route as defined in (9). To deal with such cases, Hitchcock weakens (10) by replacing the ‘active route’ in (10) with the notion of a weakly active route (2001: 290). The essential idea here that there is a weakly active route between X and Z just when Z counterfactually depends on X under the freezing of some possible, not necessarily actual, values of the variables that are not on the route from X to Z. Intuitively, to recover counterfactual dependence between Suzy’s throw and the shattering we hold fixed BT = 0: had Suzy not thrown in the model where Billy doesn’t throw, the bottle would not have shattered. Similarly for Billy’s throw.
The basic strategy deployed here to deal with both preemption and symmetric overdetermination bears an obvious similarity to Lewis’s quasi-dependence solution to the late preemption problem. Lewis resorts to quasi-dependence because the shattering of the bottle (e) does not counterfactually depend on Suzy’s throw (c), thanks to what would have happened had she not thrown (viz, Billy’s rock would have shattered the bottle instead). e quasi-depends on c, however, because of the fact that in a possible world with the same laws where the intrinsic character of the process from c to e is the same but Billy doesn’t throw, there is the required counterfactual dependence. ‘Freezing’ variables that are not intrinsic to the c-e process at their actual values (in late preemption cases) – e.g. freezing BH at 0 – turns roughly the same trick. The core difference is that Lewis’s solution involves appealing to the truth of a perfectly ordinary counterfactual (“If Suzy had not thrown, …”) at a possible world where some actual events (e.g. Billy’s hit) don’t occur, while the structural-equations solution involves appealing to the truth of a counterfactual with a special kind of antecedent (“Had Suzy not thrown and Billy’s rock still not hit, …”). Hitchcock calls these ‘explicitly nonforetracking’ (ENF) counterfactuals. (Similarly for symmetric overdetermination, where we ‘freeze’ BT at 0 – this time a non-actual value – to recover counterfactual dependence between Suzy’s throw and the shattering.)
5.2 SEF and Counterfactuals
Those who have pursued the SEF approach to providing an analysis of ‘actual’ causation – that is, the causal relation between actual, particular events – have had very little to say about the semantics of the counterfactuals that underpin SEF. Some authors (e.g. Hitchcock 2001) explicitly – and many authors implicitly – assume a broadly Lewisian approach to counterfactuals, so that the structural equations are representations of relations of facts about counterfactual dependence – as described above – whose truth conditions are broadly Lewisian.
On the other hand, one might go in the other direction, using the SEF approach to deliver the truth conditions for counterfactuals by treating the structural equations (such as SH = ST) as representations of causal dependency relationships, which in turn deliver those truth conditions (Galles & Pearl 1998, Woodward and Hitchcock 2003, Schulz 2011, Briggs 2012). Relatedly, one might eschew a Lewisian, miracle-based conception of an intervention and define interventions in explicitly causal terms (see e.g. Woodward and Hitchcock 2003: 12–13).
The choice between these two different ways of proceeding connects with the broader debate about whether causation should be analysed in terms of counterfactuals or vice versa. Lewis, of course, takes the former approach. One attraction of doing so – at least for him – is that it fits within a broadly Humean agenda: since causation is a modal notion, it threatens the thesis of Humean supervenience (Lewis 1986a, ix) unless it can somehow we cashed out in terms of similarity relations between worlds, where those similarity relations do not appeal in turn to causal (or other Humean supervenience-violating) features of worlds. Lewis’s analysis of counterfactuals, together with his analysis of laws, turns that trick. By contrast, other authors have argued that the trick simply cannot be turned: we cannot analyse counterfactuals without appealing to causation (Edgington 2011).
There are deep metaphysical issues at stake here, then: one might view the SEF approach as offering a more sophisticated variant of Lewis’s approach that shares the reductionist aspirations of that approach. Or one might – especially if one is sceptical about the prospects for those reductionist aspirations – take the SEF approach in anti-reductionist spirit, viewing it not as a way of defining causation in non-causal terms but rather as a way of extracting useful and sophisticated causal information from an inherently causal model of a given complex situation.
5.3 Models and Reality
It is a general feature of the SEF approach that the model need not include as variables all of the factors that are relevant to the effect under consideration (and indeed no model never does – there are just too many factors). In the Billy/Suzy model above, for example, there are no variables describing the actual and possible states corresponding to causal intermediaries between Billy’s or Suzy’s throwing (or not throwing) and their respective rocks hitting (or not hitting) the bottle. So what determines which variables should and should not be included in the model in order to uncover the causal relationships between the variables we’re interested in?
It’s important to stress that there is no uniquely correct model to be had for any given situation. A model that, for example, interpolated large numbers of intermediaries between Suzy’s throw and her rock’s hitting the bottle would reveal more of the causal structure of both the actual situation and various different counterfactual alternatives. But that doesn’t make it the ‘right’ model for considering the causal status of Billy’s and Suzy’s respective throws with respect to the shattering of the bottle. Such a model would deliver the same result as the simple one described above, and so the additional variables would simply be an unnecessary complication. On the other hand, there are limits on what we can leave out. For example, a causal model that just included ST and BS as variables would not deliver the result that Suzy’s throw caused the bottle to shatter, since that counterfactual is not true on this model. (To get it to come out true, we need to include BH and hold it fixed at its actual value, BH = 0.)
So what are the constraints on causal models, such that they accurately represent the causal facts that we’re interested in (Halpern and Hitchcock 2010: §§4–5)? Various authors have proposed constraints that tell us what count as (to use Hitchcock’s term) ‘apt’ models, many of which are analogues of Lewis’s constraints and for the same reasons, namely to ensure that there is no spurious counterfactual dependence. Thus Hitchcock (2001: 287) proposes that the values of variables should not represent events that bear logical or metaphysical relations to one another, and Blanchard and Schaffer (2017: 182) propose that the values allotted should represent intrinsic characterisations. Hitchcock (2001: 287) also proposes that the variables should not be allotted values ‘that one is not willing to take seriously’ (about which more below). Halpern and Hitchcock (2010) add a ‘stability’ constraint: adding additional variables should not overturn the causal verdicts. (This constraint addresses the problem of the ‘model’ described above that just includes ST and BS; that model delivers a verdict, namely that Suzy’s throw doesn’t cause the bottle to shatter, which is overturned by adding additional variables.) And Hitchcock (2007: 503) proposes the constraint that the model “should include enough variables to capture the essential structure of the situation being modeled”. (Though if one had reductionist aspirations, this constraint would appear to render one’s analysis of causation viciously circular, since the ‘essential structure’ of the situation is presumably its essential causal structure – just what a causal model is supposed to deliver.)
Precisely what the constraints should be on ‘apt’ or ‘appropriate’ models is a matter of ongoing philosophical debate (Blanchard and Schaffer 2017: §1.3). The focus here is on constraints that guarantee that a model does not deliver spurious results (e.g. that Suzy’s throw doesn’t cause the bottle to shatter). However, SEF is also used as a practical tool in scientific inquiry, and this brings additional normative questions into play concerning the choice of variables and their range of permitted values. In the context of assigning blame for the broken bottle, for example, it would not be relevant to include the strength of the bottle’s glass as a variable; by contrast, a local shop owner – tired of Suzy and Billy’s vandalism (they routinely break his shop window as well as any bottles they come across) – might be very interested in the question of what strength of glass might suffice to withstand their rock-throwing. (See e.g. Woodward 2016, Hitchcock 2017, and – for a practical example in the context of causal inference in machine learning – Chalupka, Eberhardt & Perona 2017.)
5.4 SEF and Chancy Causation
As we saw in §1.4 above, Lewis revised his 1973 account of causation to take account of chancy causation. Any account of causation that is based on the idea that causes increase the chances of their effects encounters two main problems: chance-increase is neither necessary nor sufficient for causation. (Case 1: The doctor reduces the patient’s very high chance of a heart attack by drastic surgery. Unfortunately, the surgery itself causes the patient to have a heart attack. The surgery lowers the chance of, but causes, the heart attack. Case 2: Billy and Suzy are throwing rocks at the bottle again. Each of their throws increases the chance of the bottle shattering, but Suzy’s throw pre-empts Billy’s. Billy’s throw raises the chance of, but does not cause, the bottle’s shattering.)
The first kind of case can (perhaps) be dealt with by Lewis’s modified 1973 account, by finding some intermediate event d such that the surgery raises the chance of d and d in turn raises the chance of the heart attack. But it can’t deal with the second kind of case: Billy’s throw meets Lewis’s sufficient condition for chancy causation and so the modified 1973 account erroneously counts it as a cause (Menzies 1996). This is a problem that Lewis saw for his own account and never solved: his later, 2000 account of causation as ‘influence’ assumes determinism (2000: n.1; Lewis 2004a: 79–80) and so ignores the problem. Examples of both kinds have been the subject of extensive discussion in the context of both counterfactual and probabilistic theories of causation. (For discussions about how best to deal with them within theories that don’t assume determinism, see Barker 2004; Beebee 2004a; Dowe 2000, 2004; Hitchcock 2004; Kvart 2004; Noordhof 1999, 2004; Ramachandran 1997, 2004.)
SEF accounts similarly overwhelmingly assume determinism: as with Lewis’s original 1973 account, the basic building block of such accounts is non-chancy counterfactual dependence. However there have been recent attempts to extend SEF-based analyses to cover chancy causation by Fenton-Glynn (Glynn 2011, Fenton-Glynn 2017; see also the entry on Probabilistic Causation, §4.4).
5.5 Defaults and Deviants
In §4 we saw two examples of the kinds of case that have motivated some authors to endorse contextualism. The examples exhibit different features. In the case of the theft of the coconut cake, the idea is that in different contexts of utterance, the very same causal claim – “Suzy’s theft of the coconut cake from the shop caused her subsequent illness” – can vary in truth value, depending on whether the context determines that what is at issue is Suzy’s criminality (theft rather than purchase) or, instead, which item she stole (coconut cake rather than Bath bun). The case of the gardener and the Queen, by contrast, is a case where the (alleged) cause (the gardener’s omission) and non-cause (the Queen’s) stand in the same counterfactual relationship to the effect, and yet judgements differ with respect to their causal status.
A major focus of the debate within the SEF approach has been the second kind of case – cases of what Menzies calls ‘counterfactual isomorphs’ (Menzies 2017), where two different scenarios have isomorphic causal models and yet our judgements about what causes what differs in the two different scenarios. For example, consider a case of ‘bogus prevention’ (Hiddleston 2005): believing that Killer has previously poisoned Victim’s coffee, Bodyguard puts an antidote into it. However, in fact Killer had a change of heart and didn’t poison the coffee. Victim survives – but his survival was not, surely, caused by Bodyguard’s action, for there was no threat to Victim’s life that Bodyguard neutralized. It is possible, however, to construct a causal model of this case that is isomorphic to a standard case of symmetric overdetermination: Billy and Suzy are throwing rocks again, but this time both of their throws hit the bottle at the same time, so that each is sufficient for its shattering and neither hit pre-empts the other. In that case (allegedly), we identify both Billy’s and Suzy’s throws as causes of the bottle’s shattering (Blanchard and Schaffer 2017: 185–6).
One broad line of response to the problem of counterfactual isomorphs has been to distinguish between ‘default’ (or ‘normal’) and ‘deviant’ events, and to build this distinction into the way in which causal information is extracted from the model. For example, Menzies’ approach exploits the machinery seen above with respect to Hithcock’s solution to the problem of symmetric overdetermination, which involves fixing ‘off-path’ variables at non-actual values. Menzies’ suggestion is that we fix those variables at their ‘most normal’ values, so that in effect we evaluate the relevant counterfactuals from the perspective of a world where those normal values are actualised rather than from the perspective of the actual world (Menzies 2004, 2007, 2009).
Intuitively, the basic idea is that (in the overdetermination case) the ‘most normal’ value of each of BT and ST is 0 (throwing rocks at bottles isn’t normal!), so from the perspective of a world where ST = 0, BS counterfactually depends on ST (and similarly for BT). So both Billy’s and Suzy’s throws count as causes of the bottle’s shattering. Poisoning someone’s coffee is also not normal. So we hold Killer’s failure to poison the coffee fixed (so in this case the ‘most normal’ world is just the actual world as far as the poisoning is concerned), which delivers the right result that Victim’s survival does not counterfactually depend on Bodyguard’s administering the antidote. (See Hitchcock 2007 for a different solution that trades on the default/deviant distinction.)
It is hard to see, however, how there could be a univocal and reasonably well defined notion of ‘normality’ that would deliver clear verdicts on what the ‘normal’ or ‘default’ values of variables are, and hence would deliver an objectively ‘correct’ set of models, all of which deliver the same verdict for the same situation (Blanchard and Schaffer 2017: §§2 and 3). Blanchard and Schaffer argue that ‘default-relativity’ does not solve some of the problems it was supposed to solve; more importantly, however, they argue that the alleged cases of isomorphic causal models are not really genuine cases in the first place: they arise because one (or both) of the relevant models falls foul of the independently-motivated criteria for ‘aptness’ (see §5.3 above). For example, one such criterion is that the variables not be allotted values ‘that one is not willing to take seriously’ (Hitchcock 2001: 287). But the case of the gardener and the Queen violates that criterion: the possibility of the Queen watering my flowers is, precisely, one that we do not take seriously. In other cases, they argue, the isomorphism results from deploying ‘impoverished’ models: models that fail to include enough variables to adequately represent the ‘essential causal structure’ of the situation being modelled (Blanchard and Schaffer 2017: §3).
Blanchard and Schaffer’s own view is that, insofar as our causal judgements do exhibit something like default-relativity, this is due to cognitive heuristics that engender biases in our judgements. Alternatives to ‘deviant’ events tend to ‘leap out’ at us – they are salient because they are easy to imagine – whereas alternatives to ‘default’ events don’t. Blanchard and Schaffer’s view can thus be seen as a version of invariantism, where the kinds of case that are supposed to motivate contextualism are accommodated through features of our causal talk and thought that are extraneous to the (non-norm-dependent) concept of causation.
A host of issues remain in this area. One is whether or not we should demand a uniquely ‘correct’ answer to the question of what count as ‘normal’ or ‘default’ values of variables in the first place; perhaps, if for example there are different dimensions of ‘normality’ (statistical likelihood, consonance with moral or legal norms, etc.), we should embrace the idea that two apt models of the very same situation might deliver different and equally correct results, depending on how the normal or default values are set – which in turn would depend on the context (e.g. the purpose for which the model is being deployed).
More general issues that lie in the background of the debate about ‘default-relativity’ include whether the purpose of the concept of causation is best served by an ‘egalitarian’ or ‘invariantist’ concept of causation or rather by one that takes the concept to enshrine normative considerations. Hitchcock (2017), for example, argues that since our interest in what causes what is, in essence, an interest in what kinds of intervention would bring about the kinds of results we want, we should take the latter line. A still more general issue is whether there is just one concept of causation at which all of the accounts on the table are or should be aiming, or instead several (Hall 2004, McDonnell 2018). Or perhaps causation is what Nancy Cartwright (following Neurath) calls a ‘Ballung’ concept: “a concept with rough, shifting, porous boundaries, a congestion of different ideas and implications that can in various combinations be brought into focus for different purposes and in different contexts” (2017: 136).
Bibliography
- Albert, D. Z., 2000. Time and Chance, Boston, MA: MIT Press.
- Barker, S., 2004. “Analysing Chancy Causation without Appeal to Chance-raising”, in Dowe and Noordhof 2004, 120-37.
- Beebee, H., 2004a. “Chance-changing Causal Processes”, in Dowe and Noordhof 2004, 39–57.
- –––, 2004b. “Causing and Nothingness”, in Collins, Hall and Paul 2004, 291–308.
- Beebee, H., Hitchcock, C. and Menzies, P. (eds.), 2009. The Oxford Handbook of Causation, Oxford: Oxford University Press.
- Beebee, H., Hitchcock, C. and Price, H. (eds.), 2017. Making a Difference: Essays on the Philosophy of Causation, Oxford: Oxford University Press.
- Bennett, J., 1987. “Event Causation: the Counterfactual Analysis”, Philosophical Perspectives, 1: 367–86.
- Blanchard, T. and Schaffer, J., 2017. “Cause without Default”, in Beebee, Hitchcock and Price 2017, 175–214.
- Briggs, R., 2012. “Interventionist Counterfactuals”, Philosophical Studies, 160: 139–66.
- Buckle, S., 2004. Hume’s Enlightenment Tract: The Unity and Purpose of An Enquiry Concerning Human Understanding, Oxford: Oxford University Press.
- Cartwright, N., 2017. “Can Structural Equations Explain How Mechanisms Explain?”, in Beebee, Hitchcock and Price 2017, 132–52.
- Chalupka, K., Eberhardt, F. and Perona, P., 2017. “Causal Feature Learning: An Overview”, Behaviormetrica, 44: 137–64.
- Cheng, P. and Novick, L., 1991. “Causes versus Enabling Conditions”, Cognition, 40: 83–120.
- Clarke, R., Shepherd, J., Stigall, J., Repko Waller, R. and Zarpentine, C., 2015. “Causation, Norms, and Omissions: A Study of Causal Judgements”, Philosophical Psychology, 28: 279–93.
- Collins, J., 2000. “Preemptive Preemption”, Journal of Philosophy, 97: 223–34.
- Collins, J., Hall, N., and Paul, L. (eds.), 2004. Causation and Counterfactuals, Cambridge, Mass: MIT Press.
- Dowe, P., 2000. Physical Causation, Cambridge: Cambridge University Press.
- –––, 2004. “Chance-lowering Causes”, in Dowe and Noordhof 2004, 28–38.
- –––, 2009. “Absences, Possible Causation, and the Problem of Non-Locality”, The Monist, 92: 23–40.
- Dowe, P and Noordhof, P. (eds.), 2004. Cause and Chance: Causation in an Indeterministic World, London: Routledge.
- Edgington, D., 2011. “Causation First: Why Causation is Prior to Counterfactuals”, in C. Hoerl, T. McCormack and S.R. Beck (eds.), Understanding Causation: Issues in Philosophy and Psychology (Oxford: Oxford University Press), 230–41.
- Elga, A., 2000. “Statistical Mechanics and the Asymmetry of Counterfactual Dependence”, Philosophy of Science, 68 (Supplement): 313–24.
- Ehring, D., 1987. “Causal Relata”, Synthese, 73: 319–28.
- Fenton-Glynn, L., 2017. “A Proposed Probabilistic Extension of the Halpern and Pearl Definition of ‘Actual Cause’”, The British Journal for the Philosophy of Science, 68: 1061–124.
- Frisch, M., 2005. Inconsistency, Asymmetry and Non-Locality: Philosophical Issues in Classical Electrodynamics, New York: Oxford University Press.
- –––, 2007. “Causation, Counterfactuals and Entropy”, in Price and Corry 2007.
- Galles, D. and Pearl, J., 1998. “An Axiomatic Characterization of Causal Counterfactuals”, Foundations of Science, 3: 151–82.
- Glynn, L., 2011. “A Probabilistic Analysis of Causation”, The British Journal for the Philosophy of Science, 62: 343–92.
- Hall, N., 2004. “Two Concepts of Causation”, in Collins, Hall, and Paul 2004, 225–76.
- Halpern, J. and Pearl, J., 2001. “Causes and Explanations: A Structural-model Approach – Part I: Causes”, Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence, San Francisco: Morgan Kaufman, 194–202.
- –––, 2005. “Causes and Explanations: A Structural-model Approach – Part I: Causes” (expanded version), British Journal for the Philosophy of Science, 56: 843–87.
- Halpern, J. and Hitchcock, C., 2010. “Actual Causation and the Art of Modeling”, in R. Dechter, H. Geffner and J. Halpern (eds.), Heuristics, Probability, and Causality: A Tribute to Judea Pearl (London: College Publications), 383–406.
- Hausman, D., 1998. Causal Asymmetries, Cambridge: Cambridge University Press.
- Hiddleston, E., 2005. “Causal Powers”, The British Journal for the Philosophy of Science, 56: 27–59.
- Hilton, D. and Slugoski, B., 1986. “Knowledge-Based Causal Attribution: The Abnormal Conditions Focus Model”, Psychological Review, 93: 75–88.
- Hitchcock, C., 1999. “Contrastive Explanation and the Demons of Determinism”, British Journal for the Philosophy of Science, 50: 585–612.
- –––, 2001. “The Intransitivity of Causation Revealed in Equations and Graphs”, Journal of Philosophy, 98: 273–99.
- –––, 2004. “Do All and Only Causes Raise the Probabilities of Effects?”, in Collins, Hall and Paul 2004, 403–18.
- –––, 2007. “Prevention, Preemption, and the Principle of Sufficient Reason”, Philosophical Review, 116: 495–532.
- –––, 2017. “Actual Causation: What’s the Use?”, in Beebee, Hitchcock and Price 2017, 116–31.
- Hitchcock, C. and Knobe, J., 2009. “Cause and Norm”, Journal of Philosophy, 106: 587–612.
- Horwich, P., 1987. Asymmetries in Time, Cambridge, Mass: MIT Press.
- Hume, D., 1748. An Enquiry concerning Human Understanding.
- Icard, T., Kominsky, J. and Knobe, J., 2017. “Normality and Actual Causal Strength”, Cognition, 161: 80–93.
- Kaiserman, A., 2017. “Causes and Counterparts”, Australasian Journal of Philosophy, 95: 17–28.
- Kim, J., 1973a. “Causation, Nomic Subsumption, and the Concept of Event”, The Journal of Philosophy, 70: 217–36.
- –––, 1973b. “Causes and Counterfactuals”, The Journal of Philosophy, 70: 570–72.
- Knobe, J. and Fraser, B., 2008. “Causal Judgment and Moral Judgment: Two Experiments”, in W. Sinnott-Armstrong (ed.), Moral Psychology, Volume 2: The Cognitive Science of Morality: Intuition and Diversity (Cambridge MA: MIT Press, 2008), 441–8.
- Kominsky, J., Phillips, J., Gerstenberg, T., Lagnado, D. and Knobe, J., 2015. “Causal Superseding”, Cognition, 137: 196–209.
- Kutach, D., 2002. “The Entropy Theory of Counterfactuals”, Philosophy of Science, 69: 82–104.
- –––, 2013. Causation and its Basis in Fundamental Physics, Oxford: Oxford University Press.
- Kvart, I., 2001. “Counterexamples to Lewis’ ‘Causation as Influence’”, Australasian Journal of Philosophy, 79: 411–23.
- –––, 2004. “Causation: Probabilistic and Counterfactual Analyses”, in Collins, Hall, and Paul 2004, 359–86.
- Lewis, D., 1973a. Counterfactuals, Oxford: Blackwell.
- –––, 1973b. “Causation”, Journal of Philosophy, 70: 556–67. Reprinted in his 1986a. Page references to reprinted version.
- –––, 1979. “Counterfactual Dependence and Time’s Arrow”, Noûs, 13: 455–76. Reprinted in his 1986a.
- –––, 1980. “A Subjectivist’s Guide to Objective Chance”, in R. Jeffrey, ed., Studies in Inductive Logic and Probability: Volume II, Reprinted in his 1986a.
- –––, 1986a. Philosophical Papers: Volume II. Oxford: Oxford University Press.
- –––, 1986b. “Events”, in his 1986a.
- –––, 1986c. “Postscripts to ‘Causation’”, in his 1986a.
- –––, 1986d. “Causal Explanation”, in his 1986a.
- –––, 1986e. The Plurality of Worlds, Oxford: Blackwell.
- –––, 2000. “Causation as Influence”, Journal of Philosophy, 97: 182–97.
- –––, 2004a. “Causation as Influence” (expanded version), in Collins, Hall, and Paul 2004, 75–106.
- –––, 2004b. “Void and Object”, in Collins, Hall, and Paul 2004, 277–90.
- Lipton, P. “Contrastive Explanation and Causal Triangulation”, Philosophy of Science, 58: 687–97.
- Livengood, J. and Machery, E., 2007. “The Folk Probably Don’t Think What You Think They Think: Experiments on Causation by Absence”, Midwest Studies in Philosophy, XXXI: 107–28.
- Loewer, B., 2007. “Counterfactuals and the Second Law”, in Price and Corry 2007, 293–326.
- Maslen, C., 2004. “Causes, Contrasts, and the Nontransitivity of Causation”, in Collins, Hall, and Paul 2004, 341–58.
- McDonnell, N., 2016. “Events and their Counterparts”, Philosophical Studies, 173: 1291–308.
- –––, 2018. “Making a Contribution and Making a Difference”, American Philosophical Quarterly, 55: 303–12.
- McGrath, S., 2005. “Causation by Omission”, Philosophical Studies, 123: 125–48
- Mellor, D. H., 1995. The Facts of Causation, London: Routledge.
- –––, 2004. “For Facts as Causes and Effects”, in Collins, Hall, and Paul 2004, 309–24.
- Menzies, P., 1996. “Probabilistic Causation and the Pre-emption Problem”, Mind, 105: 85-117.
- –––, 1999. “Intrinsic versus Extrinsic Conceptions of Causation”, in H. Sankey (ed.), Causation and Laws of Nature, Kluwer Academic Publishers, 313–29.
- –––, 2004. “Difference-Making in Context”, in Collins, Hall, and Paul 2004, 139–80.
- –––, 2007. “Causation in Context”, in Price and Corry 2007, 191–223.
- –––, 2009. “Platitudes and Counterexamples”, in Beebee, Hitchcock and Menzies 2009, 341–67.
- –––, 2017. “The Problem of Counterfactual Isomorphs”, in Beebee, Hitchcock and Price 2017, 153–74.
- Montminy, M. and Russo, A. (2016). “A Defense of Causal Invariantism”, Analytic Philosophy, 57: 49–75
- Northcott, R., 2008. “Causation and Contrast Classes”, Philosophical Studies, 139: 111–23.
- Noordhof, P., 1999. “Probabilistic Causation, Preemption, and Counterfactuals”, Mind, 108: 95–125.
- –––, 2004. “Prospects for a Counterfactual Theory”, in Dowe and Noordhof 2004, 188–201.
- Paul, L. A., 2004. “Aspect Causation”, in Collins, Hall, and Paul 2004, 205–24.
- Paul, L. A. and Hall, N., 2013. Causation: A User’s Guide, Oxford: Oxford University Press.
- Pearl, J., 2000. Causality, Cambridge: Cambridge University Press.
- Price, H., 1996. Time’s Arrow and Archimedes’ Point, Oxford: Oxford University Press.
- Price, H and Corry, R. (eds.), 2007. Causation, Physics, and the Constitution of Reality: Russell’s Republic Revisited, Oxford: Oxford University Press.
- Price, H. and Weslake, B., 2009. “The Time-Asymmetry of Causation”, in Beebee, Hitchcock, and Menzies 2009, 414–43.
- Ramachandran, M., 1997. “A Counterfactual Analysis of Causation”, Mind, 106: 263–77.
- –––, 2004. “A Counterfactual Analysis of Indeterministic Causation”, in Collins, Hall, and Paul 2004, 387–402.
- Schaffer, J., 2000a. “Trumping Preemption”, Journal of Philosophy, 9: 165–81.
- –––, 2000b. “Causation by Disconnection”, Philosophy of Science, 67: 285–300.
- –––, 2005. “Contrastive Causation”, Philosophical Review, 114: 297–328.
- Schulz, K., 2011. “‘If you’d wiggled A, then B would’ve changed’: Causality and Counterfactual Conditionals”, Synthese, 179: 239–51.
- Spirtes, P., Glymour, C, and Scheines, R., 2001. Causation, Prediction, and Search, 2nd edn. New York: Springer.
- Steglich-Petersen, J., 2012. “Against the Contrastive Account of Singular Causation”, British Journal for the Philosophy of Science, 63: 115–43.
- Woodward, J., 2003. Making Things Happen: A Theory of Causal Explanation, Oxford: Oxford University Press.
- –––, 2016. “The Problem of Variable Choice”, Synthese, 193: 1047–72.
- Woodward, J. and Hitchcock, C., 2003. “Explanatory Generalizations. Part I: A Counterfactual Account”, Noûs, 37: 1–24.
- Yablo, S., 2002. “De Facto Dependence”, Journal of Philosophy, 99: 130–48.
- –––, 2004. “Advertisement for a Sketch of an Outline of a Prototheory of Causation”, in Collins, Hall, and Paul 2004, 119–38.
Academic Tools
How to cite this entry. Preview the PDF version of this entry at the Friends of the SEP Society. Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers, with links to its database.
Other Internet Resources
[Please contact the author with suggestions.]


