Philolaus
Philolaus of Croton, in southern Italy, was a Greek philosopher/scientist, who lived from ca. 470 to ca. 385 BC and was thus a contemporary of Socrates. He is one of the three most prominent figures in the Pythagorean tradition, born a hundred years after Pythagoras himself and fifty years before Archytas. He wrote one book, On Nature, which was probably the first book to be written by a Pythagorean. There has been considerable controversy concerning the 20+ fragments which have been preserved in Philolaus’ name. It is now generally accepted that some eleven of the fragments come from his genuine book. Other books were forged in Philolaus’ name at a later date, and the remaining fragments come from these spurious works. Philolaus argues that the cosmos and everything in it are made up of two basic types of things, limiters and unlimiteds. Unlimiteds are continua undefined by any structure or quantity; they include the traditional Presocratic material elements such as earth, air, fire and water but also space and time. Limiters set limits in such unlimiteds and include shapes and other structural principles. Limiters and unlimiteds are not combined in a haphazard way but are subject to a “fitting together” or “harmonia,” which can be described mathematically. Philolaus’ primary example of such a harmonia of limiters and unlimiteds is a musical scale, in which the continuum of sound is limited according to whole number ratios, so that the octave, fifth, and fourth are defined by the ratios 2 : 1, 3 : 2 and 4 : 3, respectively. Since the whole world is structured according to number, we only gain knowledge of the world insofar as we grasp these numbers. The cosmos comes to be when the unlimited fire is fitted together with the center of the cosmic sphere (a limiter) to become the central fire. Philolaus was the precursor of Copernicus in moving the earth from the center of the cosmos and making it a planet, but in Philolaus’ system it does not orbit the sun but rather the central fire. The astronomical system is a significant attempt to try to explain the phenomena but also has mythic and religious significance. Philolaus presented a medical theory in which there was a clear analogy between the birth of a human being and the birth of the cosmos. The embryo is conceived of as composed of the hot and then as drawing in cooling breath immediately upon birth, just as the cosmos begins with the heat of the central fire, which then draws in breath along with void and time from the unlimited. Philolaus posited a strict hierarchy of psychic faculties, which allows him to distinguish human beings from animals and plants. He probably believed that the transmigrating soul was a harmonious arrangement of physical elements located in the heart and that the body became ensouled when the proper balance of hot and cold was established by the breathing of the new-born infant. Philolaus’ genuine book was one of the major sources for Aristotle’s account of Pythagorean philosophy. There is controversy as to whether or not Aristotle’s description of the Pythagoreans as equating things with numbers is an accurate account of Philolaus’ view. Plato mentions Philolaus in the Phaedo and adapts Philolaus’ metaphysical scheme for his own purposes in the Philebus.
- 1. Life and Writings
- 2. Basic Principles of Reality
- 3. Epistemology: The Role of Number
- 4. Cosmogony and Cosmology
- 5. Psychology
- 6. Medical Theories
- 7. Importance and Influence
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. Life and Writings
1.1 Date, City of Origin and Connections to Other Philosophers
We know very little about Philolaus’ life. Only one brief and not very reliable ancient life of Philolaus survives, that of Diogenes Laertius (VIII 84–5). Diogenes includes Philolaus among the Pythagoreans; indeed he is, in fact, one of the three most important figures in the ancient Pythagorean tradition, along with Pythagoras himself and Archytas. The central evidence for Philolaus’ date is Plato’s reference to him in the Phaedo (61d–e). Socrates’ interlocutors, Simmias and Cebes, indicate that they had heard Philolaus in Thebes at some time before the dramatic date of the dialogue (399 BC). The passage suggests that Philolaus was no longer in Thebes in 399, but there is no indication that he has died. In order for Philolaus to have been a prominent teacher by the later fifth century he must have been born no later than 440. There are other indications that he was born even earlier. Both Philolaus and Eurytus are identified by Aristoxenus as teachers of the last generation of Pythagoreans (D. L. VIII 46), who were in their twenties in 400 and active in the first half of the fourth century. Philolaus is also said to be the teacher of Eurytus (Iamblichus, VP 139), however, so that the tradition makes most sense if Eurytus is born ca. 440, and Philolaus belongs to the preceding generation and is thus born ca. 470. Such a dating would also fit with the tradition that Philolaus was the teacher of and thus somewhat older than Democritus (D. L. IX 38), who was born ca. 460. It is even less clear when he died, but one report suggests that he may still have been alive in the early 380s, when Plato first visited southern Italy (D.L. III 6). If he lived from ca. 470 to ca. 385, Philolaus is an approximate contemporary of Socrates. Plutarch’s story that as a young man Philolaus was one of two to escape the burning of the Pythagorean meeting place in Metapontum in 454 (On the Sign of Socrates 583a) would be consistent with this dating, but earlier versions of the story do not mention Philolaus (Aristoxenus in Iamblichus, VP 249–50) so that it is far from certain that he was involved in the incident.
Diogenes Laertius says that Philolaus was from the Greek city of Croton in southern Italy, but our earliest sources are divided as to his city or origin. In his history of medicine, Aristotle’s pupil Meno, who had access to Philolaus’ book, also says that Philolaus was from Croton (DK 44 A27), but another of Aristotle’s pupils, Aristoxenus, who had close connections to the Pythagoreans, presents Philolaus as from another Greek city in southern Italy, Tarentum (D. L. VIII 46, see also Iamblichus, VP 267, which probably derives from Aristoxenus). Perhaps the best way to solve the conflict is to suppose that Philolaus originally came from Croton and that, following attacks on the Pythagoreans in other southern Italian cities ca. 450 and his trip to Thebes in the late 400s, he may have settled in Tarentum late in his life. He is reported to have been the teacher of Archytas of Tarentum in one source (Cicero, de Orat. III 34.139).
The ancient tradition gives no indication of who Philolaus’ teacher(s) might have been. Pythagoras died some twenty years before Philolaus was born. He might have had some contact with the Pythagorean Hippasus (ca. 530–450?), who was associated with the mathematics of music theory, which is also a prominent theme in Philolaus. Philolaus should not be understood as simply a Pythagorean, however. He was an important philosopher in his own right, and neither Plato nor Meno bothers to apply the label Pythagorean to him. He was influenced not just by the Pythagorean tradition but also as much or more by the broader tradition of Presocratic philosophy. He was undoubtedly aware of the work of the medical writer/philosopher Alcmaeon, who also came from Croton. Anaxagoras and Empedocles were the most prominent philosophers in the generation before Philolaus, and there is some evidence that he was in part responding to Anaxagoras (see 2.1). Philolaus was the contemporary of the mathematicians Hippocrates of Chios, who was the first to write an Elements of geometry, and Theodorus of Cyrene, and, although Philolaus was not a mathematician himself, his philosophy appears to have been influenced by the important new developments in Greek mathematics that they brought about. Like most philosophers of the fifth century his work is in part a response to Parmenides (see 2.1 and 3).
1.2 The Authenticity Question
In the case of most ancient authors, the assumption is that a text handed down in their name is genuine, unless strong reasons can be given for regarding it as a forgery. This standard assumption does not apply to the Pythagorean tradition. Many more demonstrably spurious texts have survived (collected in Thesleff 1965) than texts that can with confidence be regarded as genuine. Some forgeries may have been produced for monetary reasons; a text of a “rare” work by a Pythagorean author could fetch a large sum from book collectors. There were characteristics unique to the Pythagorean tradition, however, that led to a proliferation of forgeries. Pythagoras himself wrote nothing. Starting as early as the later fourth century BC (Burkert 1972a, 53–83; Huffman 1993, 22–6), however, he came to be regarded, in some circles, as the philosopher par excellence, to whom all truth had been revealed. All later philosophy, insofar as it was true, was a restatement of this original revelation (see, e.g., O’Meara 1989). In order to support this view of Pythagoras, texts were forged in the name of Pythagoras and other early Pythagoreans, showing that they had, in fact, anticipated the most important ideas of Plato and Aristotle. These pseudo-Pythagorean texts are thus characterized by the use of central Platonic and Aristotelian ideas, expressed in technical Platonic and Aristotelian terminology. The date and place of origin of these pseudo-Pythagorean treatises is difficult to determine, but most seem to have been composed between 150 BC and 100 AD (Burkert 1972b; Centrone 1990 and 2014; Moraux 1984); Rome (Burkert 1972b) and Alexandria (Centrone 1990 and 2014) are the most likely places of origin. As a result of these unique features of the Pythagorean tradition, any fragment assigned to a Pythagorean philosopher such as Philolaus must be examined carefully before it can be accepted as genuine.
In 1962, Guthrie, in his History of Greek Philosophy, regarded the issue of the authenticity of the fragments handed down in Philolaus’ name as undecided, although he commented that opponents of authenticity did “not seem to be at their best on the subject” (331). In that same year Burkert provided decisive arguments, which have led to a consensus that a core of the fragments of Philolaus are authentic. Earlier discussions of the authenticity of the fragments were often based on the faulty assumption that the fragments were either all genuine or all spurious. Opponents of authenticity typically showed that a few of the fragments were spurious and then assumed that all the rest were as well (e.g., Bywater 1868). Given the amount of forgery in the Pythagorean tradition, however, even if fragments from a genuine book of Philolaus survive, it is likely that fragments from spurious works survive as well. Burkert made a crucial distinction between two traditions concerning Pythagoreanism. One begins already in Plato’s Academy and treats Pythagoreanism as largely identical with later Platonic thought, including the postulation of the one and the indefinite dyad as first principles (1972a, 53–83). This is the tradition which came to dominate among later Neoplatonists and which served as the basis for the production of the pseudo-Pythagorean writings. The second tradition is represented by Aristotle, who presents fifth-century Pythagoreanism as having had some influence on Plato but as radically different from Plato in making no distinction between the intelligible and sensible world (1972a, 28–52). Burkert then showed that, while some of the fragments of Philolaus did employ Platonic and Aristotelian ideas and hence were spurious, other fragments were in very close agreement with Aristotle’s account of fifth-century Pythagoreanism and hence likely to be authentic.
Aristotle’s testimony on the Pythagoreans gives rise to one remaining puzzle, which is relevant to the authenticity of the core of fragments identified by Burkert. Aristotle specifically identifies the Pythagoreanism that he discusses as contemporary with or a little earlier than the atomists (Metaph. 985b23 ff.). This dating fits Philolaus exactly. Aristotle discusses the Pythagoreans in many places and he is clearly not always referring to Philolaus. Nonetheless, the central Pythagorean metaphysical and cosmological system to which Aristotle refers repeatedly, with limiters and unlimiteds as first principles, the emphasis on the role of harmony in the cosmos and the peculiar astronomical system, which makes the earth a planet orbiting around the central fire, corresponds in great detail with the fragments and testimonia preserved in the later tradition as coming from Philolaus’ book (Metaph. 986a8–21, 987a13–17,990a8–10 etc.; for an opposing view see Zhmud 1998). The problem is that Aristotle never explicitly describes the Pythagoreanism which he discusses as derived from Philolaus’ book. He only refers to Philolaus once by name, and that is in relation to an apothegm which has no obvious connection to his general presentation of Pythagoreanism (EE 1225a30 = Fr. 16). Everywhere else Aristotle refers to the system he describes as the work of “the so-called Pythagoreans” or the Italian philosophers. The former expression shows that Aristotle has his doubts about the connections between these philosophers and Pythagoras himself. Aristotle never mentions Pythagoras himself in connection with the system of “the so-called Pythagoreans” and clearly dates that system after the time of Pythagoras. If Aristotle is relying heavily on Philolaus’ book, however, why does he never mention Philolaus by name when describing the Pythagorean system? Some might argue that Aristotle did not know of a book by Philolaus and hence that there was no such book. Two considerations suggest another explanation. First, Aristotle discusses the Pythagorean system in considerable detail and in at least one passage strongly implies that what he is reporting is based on a written text (Metaph. 1091a13). As Burkert notes, that written source cannot have been ascribed to “the so-called Pythagoreans” and must have been assigned to some author. The evidence suggests that Philolaus’ book was the only book by a Pythagorean circulating in the fifth century (see 1.3 below), and, as we have seen, the reports of the contents of that book agree with what Aristotle reports quite closely. There simply is no other plausible candidate for Aristotle’s written source. Second, Philolaus’ book seems to have been available to Aristotle’s pupil Meno (DK 44 A27–8) and hence is likely to have been available to Aristotle as well. The most reasonable conclusion is that Aristotle is relying largely on Philolaus’ book for his description of fifth-century Pythagoreanism but chooses not to refer to him explicitly. Aristotle makes clear that there are several groups of people included under the heading “so-called Pythagoreans,” by explicitly distinguishing those Pythagoreans who posited the table of opposites from the main Pythagorean system which he describes (Metaph. 986a22). For whatever reason, it was the fashion to refer to a group of related figures as Pythagoreans, and Aristotle follows this fashion rather than singling Philolaus out from the group, even though he relies heavily on Philolaus’ book. Primavesi has recently suggested that some of the puzzles about Aristotle’s account of Pythagoreanism can be mitigated if we recognize that he presents a developmental acount by reconstructing a gradual transition from early arithmological speculations to Philolaus’ theory of principles (2014).
1.3 Philolaus’ Book: Genuine Fragments and Testimonia
It is important to distinguish between two traditions regarding Philolaus’ publication of books (Burkert 1972a, 223–7; Huffman 1993, 12–15). In one tradition, which is likely to be reliable, Philolaus is reported to have published a single book, which came to bear the traditional title for all Presocratic philosophical treatises, On Nature, although it is doubtful that this title goes back to Philolaus himself. This tradition is found in Diogenes Laertius (VIII 85) but goes back to Hermippus (3rd BC) and Timon (DK 44 A8; 320–230 BC). Diogenes quotes the first sentence of this book, and it is likely that it was available to Aristotle and his pupil Meno in the fourth century (see section 1.2 above). This tradition also suggests that Plato cribbed the Timaeus from Philolaus’ book. The accusation of plagiarism on Plato’s part is absurd, but there are enough general similarities between the Timaeus and Philolaus’ book to explain the origin of the accusation (e.g., the musical scale which Plato uses in the construction of the world soul corresponds to the scale in Philolaus, Fr. 6a). This book of Philolaus is also likely to be the first book published in the Pythagorean tradition. Diogenes asserts that Philolaus was the first Pythagorean to publish a treatise on nature (VIII 85). Pythagoras wrote nothing, and we are told that the same is true of Philolaus’ immediate predecessor in the Pythagorean tradition, Hippasus (D. L. VIII 84). Some scholars argue that there were books by Pythagoreans earlier than Philolaus (Zhmud 1989 and 2012: 121–9), but, where there is clear evidence for a book, it is unlikely that the figure is a Pythagorean (e.g. Alcmaeon) and, where the figure is clearly a Pythagorean, there is no explicit evidence for a book (e.g. Hippasus). A second tradition reports that Plato bought three books from Philolaus (D. L. III 9; VIII 15 and 84). It is implied that these books were not by Philolaus himself, and it seems likely that the statement refers to three spurious works assigned to Pythagoras at D.L. VIII 6 (Burkert 1972a, 224–5). The story of Plato’s purchase of these books from Philolaus was probably invented to authenticate the three forged treatises of Pythagoras.
Burkert’s arguments (1972a, 238–277), supported by further study (Huffman 1993), have led to a consensus that some 11 fragments are genuine (Frs. 1–6, 6a, 7, 13, 16 and 17) and derive from Philolaus’ book On Nature (Barnes 1982; Kahn 1993 and 2001; Kirk, Raven and Schofield 1983; Nussbaum 1979; Zhmud 2012, Graham 2014). Fragments 1, 6a and 13 are identified as coming from the book On Nature by ancient sources. Stobaeus cites fragments 2 and 4–7 as coming from a work On the Cosmos, but this appears to be an alternate title for On Nature, which probably arose because the chapter heading in Stobaeus under which the fragments are cited is ‘On the Cosmos.’ Testimonia A7a, A9, A10, A16 (part), A17 (part), A18–24, A27–9 are also generally agreed to reflect the contents of On Nature. The authenticity of some fragments and testimonia remains controversial. Fr. 6b and Testimonium A 26, which, in contrast to Fr. 6a, take a numerological approach rather than a properly mathematical approach to music theory, were accepted as authentic by Burkert (1972a, 394–400; followed by Mueller 1997, 292–3), whereas Huffman argues that they are spurious (1993, 364–74; followed by Zhmud 1997, 185). Recent scholarship on harmonic theory argues that the conflict in approach may be less significant than it appears at first sight (see the end of section 2.2 below) and that 6b and A26 may thus be authentic (Barker 2007: 271; Hagel 2009: 143–151). Similarly, Burkert accepts A 14 as genuine and as representing the earliest evidence for horoscopic astrology in Greece (1972a, 350), whereas Huffman argues against authenticity (1993, 381–91).
1.4 Spurious Fragments and Testimonia
There are 15 fragments which are generally believed to be spurious (8, 8a, 9–12, 14, 15, 19, 20a, 20b, 20c, 21– 23) and six testimonia (11–13, 16b, 17b, 30) that are based on spurious works (Huffman 1993, 341–420). In two instances we are given titles for the spurious works from which the fragments come. Fragment 21 is said to come from On the Soul and Fr. 22 from On Rhythms and Measures. There are two problematic references to a work entitled Bacchae. Stobaeus cites Frs. 17 and 18 as coming from this work. Fr. 18, which dealt with the sun, was lost in the transmission of Stobaeus, but Fr. 17 is generally accepted as authentic on the basis of its contents and on those grounds would appear to come from On Nature. This might suggest that Bacchae was an alternative title for On Nature (Burkert 1972a, 269). On the other hand, Proclus describes the Bacchae as teaching theology by means of mathematics (DK 44 B19; Huffman 1993, 417–8), which is not a very apt description of the central surviving fragments of On Nature, but would fit the astrological material of controversial authenticity, which is cited elsewhere by Proclus (A14—see 1.3 above). Thus it may be that Bacchae is the title of a spurious work and that Fr. 17 was mistakenly assigned to that work. Kingsley argues that the title is genuine and one of several pieces of evidence for a connection between the Pythagoreans and Bacchic mysteries (1995: 262). Stamatellos (2007: 102–103) suggests that Fragments 21 and 23 are authentic, but the overwhelming consensus of other scholars regards them as spurious (see Burkert 1972: 242–243, who refers to previous scholarship and Huffman 1993: 343–344). Mansfeld (2016) suggests a quite plausible emendation to Fr. 12 but still regards it as spurious. McKirahan (2016) argues that B14 is genuine, but Philolaus’ use of psyche in the genuine B13 is incompatible with its use in B14.
2. Basic Principles of Reality
2.1 Limiters and Unlimiteds
Philolaus begins his book with a bold statement of his central insight about reality:
Nature (physis) in the world-order (cosmos) was fitted together out of things which are unlimited and out of things which are limiting, both the world-order as a whole and everything in it. (Fr. 1)
The language of this fragment shows that Philolaus is firmly in the tradition of Presocratic philosophy. Aristotle refers to the Presocratics as the physiologoi, “writers on nature,” and it is precisely nature (physis) that is the first word of Philolaus’ book. Physis here means “nature” or “real constitution” and finds a good parallel in Heraclitus’ famous saying that “nature loves to hide” (fr. 123). Philolaus uses it universally to refer to the natures of all individual things in the world as well as the nature of the cosmos as a whole. For an alternate view see Zhmud (2018) who argues that it means “all the things that have come into being and exist.” Zhmud points out that Philolaus is the first thinker to make physis the main subject of his book. The next words show that Philolaus, like his Presocratic predecessors, regarded the natural world as a cosmos, as an order, and saw it as his central problem to explain that order. His answer to that problem, however, is quite unlike earlier answers. Earlier Presocratics had tended to explain the natural world in terms of material elements such as water or air, or groups of elements such as the earth, air, fire and water of Empedocles. Opposites such as the hot and the cold or the rare and the dense also played a prominent role. Instead of these concrete and tangible substances Philolaus appeals to things which are unlimited, “unlimiteds,” and things which limit, “limiters.” The basic problem in understanding Philolaus’ philosophy is thus to determine what he means by limiters and unlimiteds. In the surviving fragments, he never provides a definition of these terms nor does he provide an explicit example. Nonetheless he uses them repeatedly. In Fragment 2 he argues that the basic elements of the world must logically be either all limiters, all unlimiteds or both limiters and unlimiteds. He is emphatic here and argues further in Fr. 3, evidently against some of his predecessors, that the basic elements cannot be simply unlimiteds. Since the world around us manifestly contains some things that limit, some that are unlimited and others that are both limiting and unlimited, we must suppose that the elements from which the world arose included both limiters and unlimiteds (Fr. 2). How could a limiter arise from an unlimited or an unlimited from a limiter? In Fr. 6 Philolaus argues that we cannot say anything more definite about the ultimate principles of reality (“nature in itself” and “the being of things”). We can only go so far as to say that they must have included limiters and unlimiteds in order for the world we see around us to have arisen. Beyond this description the basic principles of reality admit only of divine and not of human knowledge. Thus, it is a matter of principle that Philolaus does not identify any particular set of limiters and unlimiteds as the basic principles of the world; identification of such a set is beyond human capability. On the other hand, he clearly thinks that we can recognize limiters and unlimiteds in the world around us and repeatedly appeals to this fact. If the cosmos and everything in it is put together from limiters and unlimiteds, we ought to be able to identify some of them.
It is logical to begin with the very first thing that is put together in Philolaus’ cosmos. In Fragment 7 Philolaus asserts that “The first thing fitted together, the one in the center of the sphere, is called the hearth.” From other evidence we know that this hearth in the center of Philolaus’ cosmos was known as the central fire, around which all the heavenly bodies, including the earth, orbit. Since the central fire is explicitly said to have been “fitted together,” according to Fr. 1 it must have been fitted together out of a limiter and an unlimited, like everything else in the cosmos. It appears that the term “central fire” itself identifies the limiter and unlimited from which it is composed. It is composed of the unlimited fire, which is limited by its position in the center of the sphere. One interpretation then would be that unlimiteds are stuffs and limiters are shapes (Barnes 1982, 387 ff.). It is striking confirmation of this conjecture that many earlier Presocratics described their material principles as “unlimited.” Anaximander posited the unlimited as the source from which the basic material principles of the world, the opposites such as hot and cold, emerged, and his successor Anaximenes explicitly described his basic material principle air, as unlimited (DK 13 A1 and A6). Anaxagoras, in the generation before Philolaus, described all the things in the original mixture from which the world emerges as unlimited and this list would appear to include air, aither (Fr. 1), dry, wet, hot, cold, bright, dark (Fr. 4), dense and rare (Fr. 12). Thus, Philolaus’ unlimiteds probably included stuffs in the broad Presocratic sense, which treats opposites such as the hot and the cold as material substances. The next stage in Philolaus’ cosmogony after the construction of the central fire helps to identify yet more unlimiteds. In his lost work On the Pythagoreans Aristotle describes the universe as drawing in time, breath, and void from the unlimited (Arist., Fr. 201). This text certainly means that the universe was surrounded by an unlimited from which time, breath and void were drawn, but it probably also means that time, breath and void were regarded as unlimiteds. Breath can be equated with air as a typical Presocratic stuff, but time and the void show that we must expand Philolaus’ conception of unlimiteds beyond stuffs. Unlimiteds appear to be not just materials, which can appear in various shapes, but also continua, like time, which can be limited by various measures but which do not have a shape. Philolaus thus accepts the earlier Presocratic reliance on material principles but introduces two radical changes. First, he thinks it beyond human knowledge to identify any privileged set of unlimiteds, such as earth, air, fire and water, as ultimate elements. Second, he focuses not on the qualitative features of these stuffs (e.g. hot) but rather on their role as continua (Huffman 1993: 43–4; Graham 2014: 52).
Philolaus’ most significant innovation, however, is to argue that the cosmos cannot be adequately explained in terms of unlimiteds alone. There appear to be two related arguments for this thesis. First, Philolaus takes it as self-evident that the world is full of limiters such as shapes. If this is so, however, we must suppose that limiters were among the basic principles from which the world arose, since it is impossible for what limits to arise from what is unlimited (Fr. 2). Second, in Fragment 3, he argues that if all things are unlimited then “there will not be anything that is going to know.” This argument makes most sense if directed against Anaxagoras, who generates the world from elements that are all unlimited (Fr. 1), but who claims that mind (nous), which is also said to be unlimited, knows all the things that are separated off from the original mixture (Fr. 12). Philolaus seems to regard the act of knowing as an act of limitation and hence as impossible, if reality is composed just of unlimiteds (Huffman 1993, 119–120). Parmenides is the only Presocratic before Philolaus to emphasize the role of limit in his account of reality. Parmenides likens reality to a sphere and describes it as held in the bonds of a limit (DK 28 B8). Philolaus’ insistence that the ultimate elements from which the cosmos developed must have included not just unlimiteds but also limiters is best understood as an attempt to integrate Parmenides’ insights about the nature of reality with the earlier Presocratic emphasis on material elements which are unlimited (Huffman 1999). Earlier Presocratics, such as Heraclitus (DK B30, B31), had recognized that there was measure and structure in the world but no Presocratic had made structure an element or principle in the world with the same status as material principles. It is Philolaus who first insists that structure is equal in importance to material constitution (Huffman 2013b; Graham 2014: 53). Philolaus’ explanation of the cosmos in terms of limiters and unlimiteds cannot be fully understood, however, without discussing his third basic principle, harmonia.
2.2 Harmony
Already in Fragment 1, Philolaus appealed not just to limiters and unlimiteds in order to explain the world but asserted that the cosmos as a whole and everything in it only arose when limiters and unlimiteds were “harmonized” or “fitted together.” Fragment 6 is even more explicit on the need for harmony:
…since these beginnings [i.e. limiters and unlimiteds] preexisted and were neither alike nor even related, it would not have been possible for them to be ordered, if a harmony had not come upon them… Like things and related things did not in addition require any harmony, but things that are unlike and not even related … it is necessary that such things be bonded together by a harmony, if they are going to be held in an order.
Graham suggests that harmony as a principle required to allow limiters and unlimiteds to combine prefigures Platonic participation and Aristotelian ontological predication (Graham 2014: 53–4). In Fragment 6a Philolaus goes on to describe this harmony and what he describes is a musical scale, the scale known as the Pythagorean diatonic, which was used later by Plato in the Timaeus in the construction of the world soul. This scale provides Philolaus’ only surviving explicit example of the bonding together of limiters and unlimiteds by a harmony. A musical scale presupposes an unlimited continuum of pitches, which must be limited in some way in order for a scale to arise. The crucial point is that not just any set of limiters will do. We cannot just pick pitches at random along the continuum and produce a scale that will be musically pleasing. The scale that Philolaus adopts is such that the ratio of the highest to the lowest pitch is 2 : 1, which produces the interval of an octave. That octave is in turn divided into a fifth and a fourth, which have the ratios of 3 : 2 and 4 : 3 respectively and which, when added, make an octave. If we go up a fifth from the lowest note in the octave and then up a fourth from there, we will reach the upper note of the octave. Finally the fifth can be divided into three whole tones, each corresponding to the ratio of 9 : 8 and a remainder with a ratio of 256 : 243 and the fourth into two whole tones with the same remainder (for more on Fr. 6a see McKirahan 2012 and Huffman 1993: 145–165). Thus, in Philolaus’ system the fitting together of limiters and unlimiteds involves their combination in accordance with ratios of numbers. Similarly the cosmos and the individual things in the cosmos do not arise by a chance combination of limiters and unlimiteds; the limiters and unlimiteds must be fitted together in a pleasing way in accordance with number for an order to arise. Fragment 6a suggests that Philolaus saw the cosmos as put together according to the diatonic scale. This would be very much in accord with the famous conception of the harmony of the spheres according to which the heavenly bodies make harmonious music as they move, but neither in Philolaus nor any other early source do we get an explicit account of how the musical scale corresponds to the astronomical system (Huffman 1993, 279–83; Zhmud 2012: 343–4 denies that there was any connection between the harmony of the spheres and Philolaus’ system ).
Most scholars agree that Philolaus was not interested in harmonic theory for its own sake as were Archytas, Aristoxenus and much later Ptolemy (Barker 2007: 278–286; Creese 2010: 104). There is also no evidence that he used a monochord in order to determine or demonstrate harmonic relationships (Creese 2010: 104–117). However, even if Philolaus’ main interest was the application of harmonics to cosmology, the approach to harmonics found in Fragment 6a and in the disputed 6b and A26 has been of considerable interest to historians of harmonic theory, and their conclusions are highly relevant to the issue of the authenticity of 6b and A26. By the end of the fourth century there was a marked division between Pythagorean harmonic theorists who regarded musical intervals as corresponding to whole number ratios and followers of Aristoxenus who regarded them as linear magnitudes. For Aristoxenus the octave consisted of six equal tones added together and could be divided in half. For the Pythagoreans the octave was made up of ratios which were combined not by addition but by multiplication (e.g. the octave [2 : 1] = the product of the fifth [3 : 2] and the fourth [4 : 3], not the sum). The octave was a little less than six tones (9 : 8), and neither it nor the tone could be divided in halves. Fragment 6a of Philolaus mentions the ratios that correspond to the intervals (e.g., the tone is 9 : 8) whereas Fragment 6b and A26 present intervals as linear magnitudes (e.g., the tone is 27). Since 6a treats intervals as corresponding to ratios in a properly Pythagorean way, it has usually been accepted as authentic and the difference in approach found in 6b and A26 has been seen as incompatible with 6a and hence as indicative of their spuriousness. Recently some scholars, on the other hand, have suggested that in Philolaus’ time this split between regarding intervals as ratios and regarding them as linear magnitudes had not been fully developed and that Philolaus may have regarded the two approaches as compatible (Hagel 2009: 144; Creese 2010: 116, n. 119). Barker supports this point by arguing that Philolaus is employing both approaches already in Fragment 6a. Thus, while the fragment equates certain ratios with certain intervals, Philolaus does nothing mathematically with those ratios and instead emphasizes that intervals have size and can be combined to create the octave, which suggests that he thinks of them as linear magnitudes (Barker 2007: 264–271). This same combination of intervals as ratios and intervals as linear magnitudes can be seen in Fragment 6b and A26, where there is the additional emphasis on halving intervals. The halving of intervals seems to be directed at finding the mid-point of the octave and this might have been important in Philolaus’ application of the octave to the cosmos, where the center is important for the symmetry of the whole system (Barker 2007: 277; cf. Hagel 2009: 151). Moreover, Aristotle’s description of fifth-century Pythagoreanism seems to display the same odd mixture of ratios and individual numbers (Barker 2007: 286). However, there are some difficulties for this approach. While Fragment 6a does emphasize the size of intervals and their combination to form the octave, size need not mean linear magnitude and combination need not mean addition. In fact, no specific linear magnitudes (e.g. 27, which is equated with the tone in A26) are mentioned. The only sizes of intervals mentioned are precisely the ratios. Nor is there any evidence in Fragment 6a of any interest on Philolaus’ part in halving intervals. The situation is quite the reverse. He uniformly presents the octave and, indeed, all intervals as composed of unequal parts (e.g., the octave is composed of the fourth and the fifth). Thus, while it is impossible to deny that Philolaus might have tried to embrace both concepts of the nature of a musical interval, Fragment 6a still differs from 6b and A26 in being totally intelligible on the assumption that intervals correspond to ratios and in making no overt use of linear magnitudes or halves of such magnitudes (Huffman 2012: 235; cf. McKirahan 2012).
2.3 The Method of Archai
In each area of inquiry Philolaus appears to proceed by identifying the minimum number of archai, “beginnings” or “starting points,” necessary to explain the phenomena in that area (Huffman 1993, 78–92). In the case of the cosmos as a whole, as we have just seen in Fr. 6, Philolaus argues that three starting points must be assumed, limiters, unlimiteds, and harmony, as a third element to hold these two unlike elements together. In the case of disease, Philolaus identifies three archai, bile, blood and phlegm (see 6.2 below). In the case of living creatures, the brain is the starting point to which we must appeal to explain human beings, the heart as the seat of sensation is the crucial factor in explaining animals, the navel as the seat of rooting (the umbilical cord is regarded as a root) is the distinctive starting point of plants, and finally the genitals are a factor common to all animate beings in contrast to the inanimate world (Fr. 13, see 5.1). This approach to explanation seems to have been developed under the influence of contemporary mathematicians and medical writers. Graham argues that in his use of archai to mean something like “principles” Philolaus achieves “ a level of abstraction that surpasses ... probably all of his predecessors” and takes an important step towards Aristotle’s conception of archai as starting points of being or explanation (Graham 2014: 62).
3. Epistemology: The Role of Number
In the discussion of harmony above, another crucial concept in Philolaus’ philosophy emerged, number. What role does number play in Philolaus’ system? Fragment 4 provides a relatively clear answer to this question:
And indeed all things that are known have number. For it is not possible that anything whatsoever be understood or known without this.
Number plays an epistemological role; it is what allows things to be known and understood. There are several ways to interpret this claim. Some scholars have regarded “having number” as the necessary condition for the mere apprehension of an object. If something is not countable and hence distinguishable from other things, it can’t be recognized as a separate entity at all (Nussbaum 1979; Kirk, Raven and Schofield 1983, 327). The epistemological vocabulary which Philolaus uses (noein and gignôskein), however, more typically refers to understanding and knowledge than to simple apprehension of an object (Huffman 1993, 116–118). Several fragments make appeals to sense experience without mentioning the concept of number (e.g. Fr. 2), so that it would appear that Philolaus thinks that we can initially apprehend objects through our senses but that we only come to have true knowledge or understanding of them by grasping their number. Fragment 13 makes a clear distinction between sense perception, which humans and animals share, and understanding, which is limited to humans. Animals can apprehend objects in the world just as humans do, but they do not understand them because they cannot grasp the numbers which govern them, as humans can. Such an interpretation is supported by Fragment 5:
Number, indeed, has two proper kinds, odd and even, and a third from both mixed together, the even-odd. Of each of these two kinds there are many forms, of which each thing itself gives signs.
The last sentence of the fragment seems to say that individual things in the world “give signs” of the many forms of number. Our first experience of a musical scale comes through simple sense perception, but, when the phenomena are studied further, they “give signs of” or “point to” the whole-number ratios that govern the musical intervals. Once we grasp these ratios, we can claim to understand or know the scale. McKirahan (2012) argues that in Fr. 6a Philolaus formally demonstrates that ratios are numbers and that the many forms of numbers in Fr. 5 are the different types of ratios. Huffman (1993: 174) argues that Philolaus’ use of the term number includes ratios from the start and that the many forms of numbers are just the even and odd natural numbers (1993: 191; cf. 2012). Mourelatos has shown that Fragment 5 is also important in the history of the development of the concept of the universal. Philolaus distinguishes between numbers as individual species and their genera, even and odd, i.e. between subordinate and superordinate universals, as well as between numbers and things, i.e. between types and tokens, e.g. four and four pebbles. Moreover, the reference in Fragment 5 to things “giving signs” of numbers is “the first recorded attempt in the history of metaphysics at coining a term for [the relation between a particular and a universal]”(Mourelatos 2006, 66).
Burkert argues that Philolaus’ appeal to number has little to do with the rigorous mathematics that was being developed in the work of his contemporaries Hippocrates of Chios and Theodorus of Cyrene. It is instead a manifestation of the Pythagorean number mysticism, which can be found in the acusmata, the oral apothegms, many of which probably go back to Pythagoras himself (1972a, 465 ff.). Burkert sees evidence that Philolaus was not interested in rigorous mathematics in the mathematically nonsensical account of music in Fr. 6b and testimonium A26 (1972a, 394–400) as well as in what might be the use of mathematics for astrological purposes in A14 (1972a, 349–350). There are, however, independent reasons for doubting the authenticity of these texts (Huffman 1993, 364–374 and 381–391). Moreover, the mathematics of the surely authentic Fr. 6a is above reproach, and Aristotle clearly presents the interest in number displayed by fifth-century Pythagoreans as the result of their training in rigorous mathematics (Metaph. 985b23 ff.; cf. Iamblichus, Comm. Math. Sc. 78.8–18). Fragments 4 and 5 suggest that Philolaus’ program was to discover the numbers and numerical relations that govern the phenomena which we observe, and Fr. 6a suggests that the whole-number ratios which govern musical scales served as the model of the kind of mathematical account which should be supplied for all phenomena. In identifying numerical relations as the basis for knowledge Philolaus may in part be responding to Parmenides’ strictures on what constitutes a proper object of thought. Mathematical relationships certainly fit a number of the characteristics of a proper object of thought as set out by Parmenides in Fr. 8, e.g., they are ungenerated, imperishable, and unchangeable. Philolaus does not provide many further specific examples of mathematical relations controlling phenomena, which is not surprising given the scientific capabilities of the time. Indeed, the fact that the fragments and testimonia are not full of facile equations between numbers and phenomena once again suggests that Philolaus was not simply interested in symbolic connections between numbers and things and that Philolaus was looking for connections that were scientifically verifiable, as in the case of the ratios that govern musical intervals. Moreover, Greek usage shows that “having number” need not indicate just a simple one to one relation between a number and things but can also have a general sense indicating that something is constituted by an ordered plurality or relations between ordered pluralities (Huffman 1993: 175). The musical scale is one example but the alphabet may be another so that in Philolaus’ epistemology science may involve a classification and systematization of a subject that has similarities to Plato’s collection and division (Graham 2014: 55). His successor in the Pythagorean tradition, Archytas of Tarentum, appears to have adopted and been even more successful in carrying out Philolaus’ project of accounting for things in the phenomenal world in terms of number. In some cases, however, Philolaus may have been content to accept similarities between the properties of number and the properties of things. Aristotle reports that the Pythagoreans identified individual numbers with certain concepts, e.g., the number four is associated with justice (Metaph. 985b29), evidently because it is the first square number (cf. the English expression “a square deal”). It is not certain that this is a reference to Philolaus, but, when Aristotle says that the counter-earth was introduced into the Pythagorean astronomical system in order to bring the number of bodies orbiting the central fire up to the perfect number ten, this must apply to Philolaus, since the astronomical system described belongs to him (see 4.2 below). Since the world of numbers is ordered in tens, the cosmos too must parallel this order. (For further analysis of Philolaus’ use of mathematics see Huffman 1988 and 1993, 54–77.) Zhmud (2016) argues that, while Philolaus and the early Pythagoreans had some interest in the number symbolism that is found in many cultures, they did not engage in arithmology, which focuses on the special properties of the first ten numbers. Certainly it is true that there is no evidence for anything as elaborate as the the later arithmological treatises such as the Theologumena Arithmeticae. However, in order to deny any special significance for the numbers from one to ten in Philolaus one has to dismiss clear Aristotelian evidence and Philolaus’ own use of four psychic faculties and ten bodies rotating around the central fire.
There is no evidence that Philolaus thought that numbers had a metaphysical status independent of the objects which they describe (for the contrary view, i.e. that Philolaus thought that the abstract was prior to the concrete, see Netz 2005: 87–88). Aristotle emphasizes that the Pythagoreans differed from Plato in not separating numbers from things (e.g. Metaph. 987b27–9), and Plato confirms this interpretation with his criticism of the Pythagoreans on the grounds that they looked for numbers in things rather than focusing on numbers in themselves (R. 531c). On the other hand, Aristotle’s assertion that the Pythagoreans thought that things were numbers or that they were made of numbers is also not supported by the fragments of Philolaus. When describing the components of things in the world, Philolaus always talks in terms of limiters and unlimiteds and never asserts that things are made or arise from numbers (cf. Fr. 1). In the surviving fragments, number is only explicitly introduced to solve epistemological problems. It is true, however, that Philolaus’ third metaphysical principle, “harmonia,” is a “fitting together” of limiters and unlimiteds in accordance with number. Number thus does play a metaphysical role in defining the essence of things, but there is no indication that it is the material out of which they are made. Aristotle’s assertion that the Pythagoreans thought that things were numbers is best understood as his own interpretation of what Philolaus’ system amounted to (Huffman 1993, 57–64; see Schibli 1996 for a defense of Aristotle’s assertion as historically accurate). Aristotle may well have thought that if numbers are what give us knowledge of things, then, in Aristotelian terms, they are the essence of things and hence that, in a sense, things are numbers. Philolaus appears to have thought that things were composed of unlimiteds such as material stuffs and structural features such as shapes; number describes the harmonia or fitting together that defines how the limiters and unlimited were combined and hence give us the “formula” of the thing in question. There is no evidence that he addressed the metaphysical status of the numbers themselves.
4. Cosmogony and Cosmology
4.1 The Birth of the Cosmos
Fragment 7 is the beginning of Philolaus’ account of the coming to be of the cosmos:
The first thing fitted together, the one in the center of the sphere, is called the hearth.
As we would expect from Fragment 1, the world begins with a fitting together. Fragment 1 also indicates that the fitting together should involve a limiter and an unlimited. What is fitted together in Fragment 7 is “the one in the center of the sphere,” which is then called “the hearth.” From the testimony regarding Philolaus’ astronomical system (see 4.2 below) it is clear that what is in the center of Philolaus’ cosmos is the central fire, and surely it is the central fire that is called the hearth in Fragment 7. What are the limiter and the unlimited from which the central fire is put together? Fire is the obvious choice as the unlimited element, and it is limited by being placed at the center of a sphere. Aristotle tells us that the next step was for the nearest part of the unlimited to be drawn in (Metaph. 1091a17), and elsewhere he specifies that it is time, breath and the void, which are drawn in from the unlimited (Arist., Fr. 201). Evidently then Philolaus first envisaged the emergence of a sphere with a fire at its center. As in most Presocratic cosmologies, the cosmos is surrounded by an unlimited expanse, and Philolaus’ central fire draws in time, breath and void from that expanse. Each of these three is itself an unlimited, a continuum not yet limited in any way. Like many other Presocratics Philolaus drew an analogy between the birth of the cosmos and the birth of a human being. At birth the human embryo, which is hot, breathes in cooling air just as the central fire draws in cooling breath from the unlimited. It may be that the interaction of hot fire and cold breath was thought to generate the other prominent stuffs in the world such as earth and water. Void serves to distinguish individual things from each other spatially (Arist., Fr. 201); bits of the central fire were perhaps separated off to form the sun, stars and planets. Time provides the temporal continuum in which the cosmos can develop and according to which the periods of the planets can be measured (see Zhmud 1998 for doubts that time should be included in the cosmology but note that Aristotle refers to time outside the cosmos not only in Fr. 201 but also at De Caelo 279a12, although without specifically mentioning the Pythagoreans). Some have argued that this cosmogony does not distinguish breath and void, since they are drawn in together, and hence that at least this element of the cosmogony is archaic and dates before Philolaus, since it must antedate Anaxagoras, who first made the distinction (Kahn 2001, 37). Breath and void are listed separately, however, along with time as three things drawn in, and there is no obvious reason to assume that the first two are being identified. Moreover, breath and void serve different functions in the cosmogony (cooling and the spatial differentiation of objects), so that it appears more likely that they are not being equated and that Philolaus developed the cosmogony after void and air had been first distinguished by Anaxagoras and Empedocles. Fragment 17 provides us with the only further evidence for Philolaus’ cosmogony, asserting again that the cosmos began to come to be at the middle and adding that it developed symmetrically around the middle. The end of the cosmogony is the astronomical system described in section 4.2 below, in which ten heavenly bodies including the earth encircle the central fire.
There is considerable controversy about the role of number in this cosmogony. Some scholars argue that the generation of the cosmos is also the generation of numbers and that the central fire is the number one and other heavenly bodies are identified with other numbers, e.g., the sun is seven (Kahn 2001, 28; Schibli 1996). Thus, in Fragment 7, when Philolaus refers to “the one in the center of the sphere,” he is not referring simply to the central fire as the first unity of limiter and unlimited but also to the number one. The strongest support for this view is Aristotle’s assertion that the Pythagoreans “clearly state that the one was constructed… and then that the nearest part of the unlimited was drawn in” (Metaph. 1091a15 ff.). Aristotle is complaining about the absurdity of supposing that there can be a generation of eternal things such as numbers, and he appears to be taking Fr. 7 as a clear statement by the Pythagoreans that the number one is generated. The difficulty with accepting this view is that it seems unintelligible to say that the central fire and the number one are the same thing. It is quite plausible to assume that there is an analogy between the central fire as the first thing in the cosmos and the number one as the first of the numbers, but the claim is that the number one is identical with the central fire, and it would follow that the number one is a large fire at the center of the cosmos surrounded by ten heavenly bodies. The context of Aristotle’s assertion that the number one was constructed shows, moreover, that there was considerable controversy as to whether or not the Pythagoreans were to be interpreted in this way and that Aristotle is taking sides in a debate; he says that “it is not necessary to doubt” his assertion, which implies that some have indeed doubted it. The evidence he cites for his own position appears to be precisely Fr. 7, and there seems to have been little clear evidence on the issue; Aristotle complains that the Pythagoreans do not say of what the number one is composed and suggests planes, surfaces and seeds as possibilities. It thus does not appear that Aristotle was drawing on any other more explicit statement than what we find in Fr. 7, and his remarks indicate that the interpretation of Fr. 7 was controversial even in his own time. None of the other fragments of Philolaus equate numbers with things in this way, and Fr. 5 asserts that things “give signs of” or “point to” numbers rather than that they are identical with numbers (see section 3 above). This evidence suggests that in Fr. 7 Philolaus is not asserting that the number one was generated but is instead describing the generation of the first unity of limiter and unlimited, the central fire (Huffman 1993, 202–215; followed by Zhmud 2012: 400).
4.2 Astronomical System
Philolaus’ astronomical system is famous as the first to move the earth from the center of the universe and make it an orbiting planet instead. Copernicus referred to Philolaus as his precursor in the preface to his De Revolutionibus (see Kahn 2001, 26 for references). Unlike Copernicus, however, Philolaus did not replace the geocentric with a heliocentric universe. The central fire rather than the sun is at the center of Philolaus’ cosmos. The heavenly bodies are arranged in ten concentric circles around this central fire. Beginning from the outside, the fixed stars come first, then the five planets, the sun, the moon, the earth and a mysterious counter-earth. The system can account for the basic phenomena with elegant simplicity. The fixed stars serve as the backdrop against which the other heavenly bodies move. All of the bodies have only one circular motion around the central fire, from west to east. The moon completes its orbit in about a month, the sun in a year and each of the planets has its own period of revolution. Thus, bodies move more slowly, the farther removed they are from the central fire,and the fixed stars probably did not move at all. These motions account for the basic apparent movement of the sun, moon and planets through the zodiac, although there is no attempt to explain more sophisticated planetary phenomena such as retrograde motion, where the planet appears to stop and move backward before continuing its progress through the zodiac. Retrograde motion was only first addressed almost a century after Philolaus by Eudoxus. The earth has by far the fastest motion, completing a circuit of the central fire in 24 hours. It is the motion of the earth that accounts for the apparent daily motion of the sun across the sky and hence for night and day. The much faster moving earth, which rotates on its axis so as to keep our side always turned away from the central fire and counter-earth (see below), leaves the sun behind so that day lasts as long as the earth is facing the sun, and night occurs when the earth turns away from the sun as it moves around the central fire.
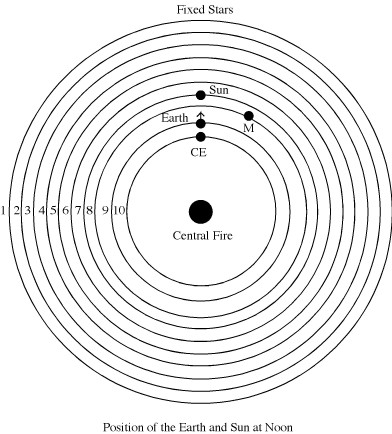
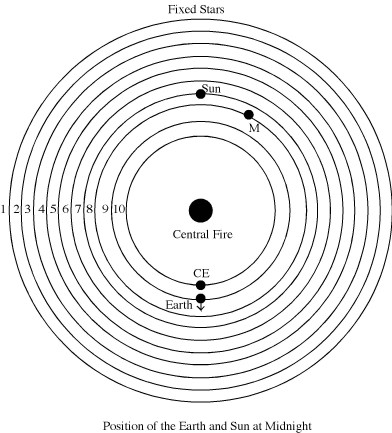
The system is the result of a combination of a priori principles and reliance on observation. Philolaus is the first to incorporate all five planets commonly known in antiquity into an astronomical scheme in the correct order, which indicates that he was aware of the most up-to-date astronomical data (Eudemus as cited in Simplicius, in De Caelo 471.4; Huffman 1993, 260; Zhmud 2012: 336–7 thinks that Eudemus is referring to an earlier Pythagorean system). On the other hand, there are a number of features that appear to be explained by appeal to a priori principles of order. Thus, moving the earth from the center of the universe did not serve to explain astronomical data better. There is no explicit reason given for moving the earth; Aristotle reports that some others (Platonists?; see Kingsley 1995, 175–80) thought it should be moved because fire was thought to be a “better” element than earth and hence to belong at the center of the cosmos, which is a position of honor (Arist., De Caelo 293b2). We are explicitly told that the Pythagoreans accepted one of the premises of this argument, that the center is the most important part of the cosmos (Arist., De Caelo 293b2–3), and it is likely that the whole argument should be assigned to Philolaus (Huffman 2007, 76–80). This is consistent with the evidence of Frs. 7 and 17, which clearly indicate that the cosmogony began in the center. Philolaus may have assigned fire the position of honor, because of the analogy with human birth, since he argued that the human embryo develops from the hot (see 5.3 below). The case of the counter-earth is more complicated. Aristotle suggests that it was introduced for a priori reasons: to raise the number of heavenly bodies around the central fire from nine to ten, which the Pythagoreans regarded as the perfect number (Arist., Metaph. 986a8–12; on the other hand Zhmud 2012:407 argues that the number ten had no particular significance for the Pythagoreans). Some scholars have objected that, if we count the central fire, the introduction of the counter earth makes eleven bodies in Philolaus’ system (Burch 1954, 284; Kingsley 1995, 174); the ancient evidence consistently talks in terms of bodies arranged or moving around the central fire, however, and obviously the central fire cannot be counted as one of these (Aetius 2.7.7; Arist., Fr. 203 and Metaph. 986a10), so that Aristotle’s explanation retains considerable plausibility (Burch 1954 suggests that the counter-earth was introduced as a counter-weight to the earth, so that the center of gravity of the cosmos would coincide with the spatial center, but there is no evidence that Philolaus had the concept of a center of gravity). On the other hand, Aristotle also comments that the counter-earth was introduced to explain lunar eclipses (De Caelo 293b18–25). Graham has recently made a convincing case that the counter-earth could in fact account for eclipses of the moon at dawn and dusk, which otherwise would be inexplicable on Philolaus’ model (Graham 2015, see also Graham 2014: 57–60). Graham speculates that the term for counter-earth in Greek (antichthon), may refer to the counter-earth’s “taking the place” (anti) of the earth in accounting for these lunar eclipses, which cannot be explained by the interposition of the earth (Graham 2015: 229). Thus, one of the main features of Philolaus’ system that had been thought to show its non-scientific character, may, in fact, be motivated by an attempt to make the system better explain the phenomena. The doxography also assigns the counter earth to the Pythagorean Hicetas (DK 50A2; cf. Mansfeld 2010a: 90–93). The fixed stars do not literally move in Philolaus’ system but they, like the planets, sun and moon, have an apparent diurnal movement caused by the motion of the earth. Even Philolaus’ basic assumption that the cosmos is spherical (Frs. 7 and 17) may be based on Parmenides’ a priori arguments that reality is similar to a sphere in perfection (Fr. 8.42–44).There is no explicit statement about the shape of the earth in Philolaus’ system and some have supposed it to be flat (Burch 1954: 272–273). Analogy with the cosmos suggests that it was spherical as well and several of Aristotle’s descriptions of the Philolaic system show that it was (Dicks 1970: 72–73). Philolaus appears to have believed that there was also fire at the periphery of the cosmic sphere and that the sun was a glass-like body which transmitted the light and heat of this fire to the earth, an account of the sun which shows connections to Empedocles; Philolaus also posited a great year of 59 years in which the lunar and solar cycles were reconciled (Huffman 1993, 266–70 and 276–279). Philolaus’ great year may be connected to the doctrine of the periodic return of all things, which Dicaearchus assigns to the Pythagoreans (Porphyry, Life of Pythagoras 19), which may be in turn a generalization of reincarnation (Riedweg 2005, 63).
As in the case of Philolaus’ cosmogony, there is considerable controversy about the precise nature of Philolaus’ astronomy. The a priori features, as well as other testimonia stating that Philolaus believed that the moon was inhabited by creatures fifteen times more powerful than those on the earth (Aetius 2.30.1 = DK 44 A20), have suggested to some that Philolaus’ system is largely a fantasy and has nothing to do with empirical astronomy (Furley 1987, 58). Burkert argues, moreover, that the apparent coherence of the astronomical system is destroyed, because the fixed stars, which serve as the backdrop for the motions of the heavenly bodies described above, were not in fact stationary but moved with the fastest motion so that, without a fixed backdrop, the whole system dissolves into chaos (1972a, 340); he argues that Philolaus’ astronomy is primarily of mythological and religious significance (1972a, 348). However, more recent assessments argue that Philolaus’ astronomical system was a serious attempt to account for the phenomena and the most successful such attempt of his time (Huffman 1993: 231–288; Graham 2015). The text on which Burkert relied to conclude that the fixed stars have the fastest motion is, in fact, part of a speculative reconstruction of the doctrine of the harmony of the spheres by a later Greek commentator, Alexander of Aphrodisias, and not a description of Philolaus’ system. Nor need speculation about the inhabitants of the moon indicate that the system is fantastical, since such staid Presocratic rationalists as Anaxagoras also argued that the moon was inhabited (see D.L. II 8 and DK 59 A77). Perhaps the strongest reason for believing that Philolaus’ astronomical system was at least in part an attempt to explain the phenomena rather than just of religious and mythological significance is that other thinkers made objections to the system on empirical grounds, and Philolaus responded to those criticisms in ways that attempted to show that his system could explain or “save” the phenomena. Thus an obvious objection to the system is that we never observe the central fire at the center of the universe. Philolaus explained this by supposing that the earth rotates once on its axis as it orbits the central fire, so that our side of the earth is always turned away from the central fire and hence we never see it. This is also why we never see the counter earth, which is evidently supposed to move at the same speed as the earth. An objection to the moving earth was raised on the grounds that the parallax produced by its movement from one side to the other of the central fire would cause the sun, moon and planets to appear to move in ways in which they do not. Philolaus evidently argued that the diameter of the earth’s orbit was so small relative to the distance to the other heavenly bodies that the parallax effects would be negligible (De Caelo 293b25–30). It is not clear that this solves the problem, but if the system is solely of mythic or religious significance it is odd that other thinkers, including Aristotle, treated the system as if it were supposed to be consistent with the phenomena, and even more surprising that Philolaus tried to defend the system by showing that it was consistent with those phenomena. Moreover, as mentioned above, Graham has recently shown that the counter-earth is not introduced just for a priori reasons but serves to give the most sophisticated account of lunar eclipses of the time (Graham 2015).
Comparison between the cosmology of the oral sayings ascribed to Pythagoras (the acusmata) and Philolaus’s cosmos shows that Philolaus’ system represents the transition from a cosmology that is primarily mythical to one that is primarily rational and scientific (Huffman 2013a). It remains possible that, while the system is intended to save the phenomena, some of its features may retain religious significance as well; some have argued that the counter-earth might be connected to a realm common in folklore where everything is “counter” to our world, a realm that often has connections to the world of the dead, Hades (Burkert 1972a, 347–8; Kingsley 1995, 186–7), but there are not good parallels for such a conception of Hades in the Greek tradition. Kingsley argues that the central fire is to be equated with Tartarus, a region even below Hades in Greek myth, and that the introduction of the counter earth and central fire is largely inspired by interpretation of Homer’s description of Hades and Tartarus as below the earth; Aristotle attests that the Pythagorean name for the central fire was Dios phylakê, which Kingsley translates as “prison of Zeus,” which would accord with Tartarus’ function as the prison in which the Titans as well as humans damned to punishment were kept (1995, 183 ff.). The text on which Kingsley relies (Anatolius, On the Decad 6.13 Heiberg) does not mention Philolaus by name, however, and is not, in fact, likely to be referring to Philolaus. Moreover, Philolaus calls the central fire “the hearth,” whose positive connotations as the religious center of the house and state are hard to reconcile with its being the place of punishment, Tartarus. In addition, parallels show that, in the fifth and fourth century, the name Dios phylakê refers to a garrison that guards Zeus or his palace rather than to a prison (Plato, Protagoras 321d). In mythical terms it thus appears that Philolaus conceived of the central fire as the fire that Zeus kept guarded in his palace and that Prometheus stole and gave to humanity. Philolaus’ cosmogony, in which the central fire draws in void and thus separates off parts of fire and spreads them to the rest of the cosmos thus replicates Prometheus’ theft in naturalistic terms. This connection to myth is confirmed by Plato’s description of Philolaus’ metaphysical system as hurled down from the gods to men by some Prometheus (Philebus 16c), but it is hard to know what religious significance Philolaus saw in the myth (see Huffman 2007 for a response to Kingsley’s points).
Betegh (2014: 162–6) has recently argued that while Philolaus’ system does make sense as a contribution to the tradition of rational Presocratic cosmology it at the same time incorporates and reinterprets elements of the religious tradition concerning the hearth. Thus, the hearth was the center of the household and putting a hearth at the center of the cosmos suggested that it was analogous to the household. The ritual by which the newborn child was carried around the hearth to introduce it into the household is now paralleled by the planets motion around the central fire. Moreover, Betegh argues that the Orphic tradition represented by the Derveni papyrus shows a similar tendency to give a new religious relevance to concepts derived from natural philosophy. He also argues that there are striking similarities between the cosmological theories of the author of the Derveni papyrus and Philolaus, partcularly in the role of fire. At the same time it is noteworthy that whereas the Derveni author presents a demiurgic mind as ordering the cosmos, Philolaus never explains what brought limiters and unlimiteds together to form the cosmos (on this lack of an efficient cause see also Graham 2014: 65–6).
5. Psychology
5.1 Psychic Faculties
Fragment 13 presents Philolaus’ account of psychic faculties:
The head [is the seat] of intellect, the heart of soul (psychê) and sensation, the navel of rooting and first growth, the genitals of the sowing of seed and generation. The brain [contains] the origin of man, the heart the origin of animals, the navel the origin of plants, the genitals the origin of all (living things). For all things both flourish and grow from seed.
Philolaus thus recognizes four distinct psychic faculties. He makes a clear distinction between intellect (nous), which is limited to human beings, and perception, which animals possess as well. He has no word for the soul as a whole and uses psychê, which serves this function in Plato and Aristotle, for the psychic functions shared by humans and animals. Some have argued that for Philolaus psychê only meant “life,” a common use in the fifth century (Burkert 1972, 270). However, since plants are alive and psychê is not assigned to them, “life” is not a good translation. Parallels in Herodotus suggest that for Philolaus psychê was the seat of emotions and desires, which was closely connected to perception (Huffman 2009). The third psychic faculty is responsible for nutrition and growth and the fourth governs generation and the sowing of seed. This hierarchy of four faculties is strikingly associated with the hierarchy of living beings (human, animal, plant) as well as a hierarchy of parts of the body (head, heart, navel, genitals). In identifying the head as the seat of intellect, Philolaus is siding with his fellow townsman, Alcmaeon, against those like Empedocles who championed the heart. He goes beyond this controversy to locate each faculty in a part of the body and thus anticipates a similar attempt by Plato to assign psychic faculties to regions of the body in the Timaeus. Philolaus makes a significant advance over earlier Presocratics by making a firm distinction between thinking and perception. His systematization of psychic faculties goes beyond anything found in his predecessors and is the recognizable precursor of Aristotle’s distinction between the faculties for nutrition, appetite, sensation, movement and thought (de An. 414a31–2). Riedweg notes that three of the seats of the psychic faculties (brain, heart and genitals) in animals are forbidden to be eaten in the acousmata, so that it may be that a connection can be seen here between scientific and religious strands in Pythagoreanism (2005, 110).
5.2 Soul as a Harmony
Macrobius (5th century AD) is the only ancient source to attribute to Philolaus the doctrine that the soul is a harmony (DK 44 A23). It is not clear that this ascription is based on anything in Philolaus’ book, moreover, and it may just be a conclusion based on the espousal of the doctrine by Simmias, who is presented as a pupil of Philolaus, in Plato’s Phaedo (86b5 ff.). The doctrine as presented in the Phaedo may be Plato’s invention based on several Presocratic sources (Mansfeld 2010b: 183–188). However, since Philolaus believed that all things were either limiters, unlimiteds or harmonious combinations of limiters and unlimiteds, it is not implausible that he would have regarded soul as such a harmony of limiter and unlimited. In Fr. 13 soul (psychê) is the center of emotions and desires, is associated with sense perception, and has its seat in the heart (see 5.1 above). Sedley argues that Philolaus’ embryology (see 6.1 below) suggests that a body is first ensouled when the heat (an unlimited) of the embryo was cooled, and hence limited, by breath. The soul can thus be viewed as a harmony of these and other opposites, which is the view that Simmias presents in the Phaedo (Sedley 1995, 22–6). In the Phaedo, however, the view that the soul is a harmony of parts of the body is shown to be in conflict with its immortality. Some have thus thought that Philolaus did not believe in the immortality of the soul or transmigration (see now McKirahan 2016). It is more likely, however, that he regarded the psychê, which was the center of desires and emotions located in the heart and shared with animals, as a harmony of its own material elements. This may have been drawn in with the first breath of the infant and from its seat in the heart it may have served as the command center which establishes the harmony of hot and cold which makes the body ensouled. After the body loses its harmony and dies, this command center soul survives to transmigrate into the hearts of other animals and men. If the psychê was the transmigrating soul for Philolaus, it follows that he did not think that humans were reborn as plants, since according to Fr. 13 plants do not have a psychê. Moreover, it would only be the human character as constituted by emotions and desires that transmigrates and not human intellect, since according to Fr. 13 psychê does not include intellect (Huffman 2009; for a critique see Palmer 2018).
6. Medical Theories
6.1 Embryology
We would never have known that Philolaus had contributed to medical theory if not for the papyrus known as the Anonymus Londinensis, which is in part based on the history of medicine written in the late fourth century BC by Aristotle’s pupil Meno (DK 44 A27–8; Huffman 1993, 289–306). Philolaus is one of twenty thinkers whose views on the causes of disease are presented in the papyrus, and the relatively detailed presentation of Philolaus’ views suggests that Meno had access to his book. Philolaus is included among those thinkers who argue that diseases arise from the elements which constitute the body, so that the section on Philolaus begins with his account of the constitution of the human body, which is in effect his account of the nature of the embryo and newborn infant. Philolaus is unusual in arguing that the embryo is composed of just one element, the hot, and has no cold in it. The embryo must be hot because both sperm and the womb, in which the sperm is deposited, are hot. Immediately upon birth, our bodies, which were too hot before, draw in cooling breath, which is then sent out again “like a debt.” Thus, respiration suggests that the cool air which is drawn in was originally something foreign to the body, which must be paid back to the source from which it is drawn. The limitation of the body’s innate heat by cooling breath may be the process by which the body becomes ensouled (see 5.2 above). There is a clear analogy between the embryo, constituted solely of the hot, breathing in cooling air and the central fire drawing in breath from the unlimited in the early stages of Philolaus’ cosmogony (see 4.1).
The evidence for Philolaus’ embryology discussed above (DK 44 A27–28) does suggest that he, like Anaxagoras, believed that only the male contributed seed and that the female was simply the place in which the seed was sown. Some scholars have gone further and argued that Philolaus subscribed to the view that the seed arose from the brain and the spinal marrow and had hot breath in it, which conveyed soul to the child (Leitao 2012: 29–30). However, this interpretation is based on Diogenes Laertius 8.28, which does not mention Philolaus by name and in fact derives from the Pythagorean Memoirs excerpted by Alexander Polyhistor. This treatise is believed by most scholars to belong to the later pseudo-Pythagorean tradition and hence is not good evidence for Philolaus’ beliefs (Burkert 1972: 53). Moreover, the report contradicts the genuine fragments of Philolaus in a number of ways. Fragment 13 of Philolaus asserts that semen comes from the genitals not the brain and A27 clearly suggests that seed is composed just of the hot, says nothing of its origin in the brain, and indicates that breath does not enter the child through the male seed but only when it is drawn in upon birth.
6.2 Disease
The Anonymus Londinensis then tells us that Philolaus explained disease in terms of three factors: bile, blood and phlegm. It is surprising that no mention is made of the basic constituent of the body, the hot, since Philolaus is presented as one of the thinkers who explains disease in terms of the constituents of the body (see 6.1 above). It may well be, however, that bile, blood and phlegm were all regarded as hot, since blood and bile were typically regarded as hot, and we are explicitly told that Philolaus argued that phlegm was hot, although it was typically regarded as cold (Lloyd 1963, 120). Moreover, excesses and deficiencies of heat, cold and nutriment are also said to be causes of disease. It would appear then that health depends on appropriate cooling of the natural heat of the body and that bile, blood and phlegm cause disease insofar as they are not constituted properly by the balance of heating and cooling, the balance of which can also be upset by improper nutrition. There are a number of puzzling features in Philolaus’ presentation of the three humours: blood, bile and phlegm (Gourevitch 1989, Manetti 1990). Phlegm is said to be constituted from ombroi, which usually means “rain storms,” but probably here means just liquids (Manetti 1990). However, Manetti’s suggestion (1990) that phlegm does not refer to the humour but rather means “inflammation” is not very likely, since phlegm is not said to be caused by the liquids, which is what we would expect if it meant “inflammation” but rather constituted of them. Philolaus’ account of disease may be distorted by the intervention of the author of the Anonymus Londinensis (Manetti 1990).
7. Importance and Influence
7.1 Philolaus and Pythagoras: How original is Philolaus?
Pythagoras is one of the most famous names in the ancient philosophical tradition, and there is a natural tendency to assume that he was responsible for the most fruitful ideas in the Pythagorean tradition. One of the dominant trends in recent scholarship on Pythagoras, however, is to recognize that his fame grew exponentially with the passage of time and that the early evidence, down to the time of Plato and Aristotle, when examined carefully, reveals that Pythagoras was indeed famous but not as a typical Presocratic cosmologist nor as a mathematician/ scientist. In the early tradition Pythagoras is consistently presented as a charismatic teacher famous for two things: 1) his expertise on the fate of the soul in the next life as represented in the doctrine of transmigration of souls 2) his founding of a way of life which some people still followed a hundred years after his death. This way of life involved moral and religious teachings that were embodied in a series of brief sayings known as acousmata, which included ritual taboos and dietary restrictions such as the famous prohibition on eating beans (Burkert 1972a, 166–92). There is no evidence that Philolaus made any significant contribution in these areas. Plato’s suggestion in the Phaedo that Philolaus had something to say about the prohibition against suicide is the closest we get to a pronouncement on how to live one’s life. It seems most reasonable to assume that he followed, to a greater or lesser degree, the Pythagorean life handed down from the time of Pythagoras, who died some twenty years before Philolaus was born. There are a few hints that he tried to reconcile the mythic and religious side of Pythagoreanism with his own naturalistic explanation of the world (see 4.2 and 5.1 above).
On the other hand, Aristotle always presents the philosophical system of limiters and unlimiteds, which placed an emphasis on the role of number in understanding the cosmos and which included the astronomical system built around the central fire, as the work of “the so-called Pythagoreans,” whom he dates to the second half of the fifth century, at the same time as or a little earlier than the atomists (e.g. Metaph. 985b23 ff.). This is the philosophical system that we find in the fragments of Philolaus, and Aristotle’s dating fits Philolaus exactly so there can be little doubt that Philolaus was the leading figure among those labeled “the so-called Pythagoreans” by Aristotle. Although some scholars continue to argue that most of what Aristotle ascribes to “the so-called Pythagoreans”should be regarded as Pythagoras’ own teaching (Riedweg 2005, 77–80), Aristotle’s testimony doubly distances Pythagoras himself from the Philolaic system. First, Aristotle is emphatic that the system dates after the time of Pythagoras, and second, his expression “so-called Pythagoreans” is most reasonably understood to suggest that, although he knows that the name “Pythagorean” is often given to Philolaus and his contemporaries, he can see little reason to connect the philosophical system they espouse to Pythagoras himself. The later tradition also emphasizes Philolaus’ originality in the area of cosmology by asserting that he was the first Pythagorean to publish a work on nature (D. L. 8.85). The testimony of Aristotle and the later tradition is largely confirmed by the content of Philolaus’ philosophy. Although the contrast between limit and unlimited is implicit from the beginning of the Presocratic tradition, the first explicit champion of limit is Parmenides, and the attempt to explain the world in terms of a combination of limiters and unlimiteds thus makes most sense as arising after Parmenides has championed limit (Huffman 1999). Moreover, the style of argumentation in Fragments 1–6, and particularly Fr. 2, is reminiscent of Parmenides and his successor Melissus (Kahn 2001, 34), so that the central metaphysical system and the arguments for it look very much as if they are the original contribution of Philolaus. The same is true of the astronomical system built around the central fire, which the later tradition assigns to Philolaus and which Aristotle (Metaph. 986a8 ff.) and Fr. 7 explicitly tie to the philosophy of limiters and unlimiteds. Kahn is inclined to regard parts of the cosmogony as going back to Pythagoras. He argues that the idea of the cosmos breathing is archaic and that it may have been attacked long before Philolaus by Xenophanes, who pointedly describes his god as not breathing; Kahn also argues that the equivalence between air and void suggests a date before Anaxagoras (2001, 36–7). In section 4.1 above, however, reasons have been given to show that the Philolaic system, in fact, distinguishes between air and void and hence once again conforms very well to Philolaus’ date after Anaxagoras. The breathing of the cosmos need not be seen as archaic, since biological analogies are still found in the cosmogony of the atomists (DK 67 A1). Xenophanes’ remark is reported in only one testimonium (DK 21 A1) and is not found in any of the extant fragments of his book; if it is his, it need not be directed at anything other than general Greek anthropomorphism.
The question remains whether or not Pythagoras had adumbrated any sort of cosmology and what the relation of that cosmology was to Philolaus’ later system. It is certainly true that the discovery that the primary musical concords of the octave, fourth and fifth are governed by the simple whole number ratios 2 : 1, 4 : 3 and 3 : 2 occurred before Philolaus. Most of the traditions connecting this discovery to Pythagoras himself, however, are unreliable; Hippasus is the earliest Pythagorean connected to a scientific demonstration of these phenomena, but the actual discovery probably antedates him and may not be specifically Pythagorean (Huffman 1993, 147–8). It is also true that number plays a significant symbolic role in the acousmata that go back to the time of Pythagoras. Thus one of the acousmata asserts that number is the wisest thing (Iamblichus, On the Pythagorean Life 82). Pythagoreans took oaths in the name of Pythagoras as “the one who gave the tetraktys”—tetraktys being a name for the first four numbers, whose total is ten, which was the perfect number for the Pythagoreans. Our evidence for the oath is late, but the acousmata refer to the tetraktys as “the harmony in which the Sirens sang” (Iamblichus, On the Pythagorean Life 82), which may indicate an awareness of the role of the first four numbers in the whole-number ratios which determine the musical concords. The harmony in which the Sirens sing could be a reference to the famous doctrine of the harmony of the spheres, according to which the heavens make music by their motions. The acousmata also adumbrate a cosmology which is tied to a religious doctrine of reward and punishment. The planets are described as the avenging hounds of the goddess Persephone (Porphyry, Life of Pythagoras 41), the sun and the moon are the isles of the blessed, where the good may be sent as a reward (Iamblichus, On the Pythagorean Life 82), and thunder is a warning to souls in Tartarus (Aristotle, Posterior Analytics II, 11 94b33). It appears then that Pythagoras had presented a vision of the cosmos which was ordered according to symbolic numbers and which reinforced certain religious ideas (West 1971, 213–18). Philolaus continues in this tradition by arguing that there are ten celestial bodies arranged around the central fire, because ten is the perfect number, and also by perhaps endowing some of the parts of his cosmos with mythological and religious significance, e.g., by equating the central fire with the fire guarded by Zeus and stolen by Prometheus (see 4.2 above). On the other hand Philolaus’ attempt to save astronomical phenomena by including the five planets in correct order according to their periods, by giving an explanation of night and day and by responding to concerns about how parallax might affect the way the heavenly bodies appear to move has no apparent precedent in the cosmology of the acousmata. It would thus appear that Pythagoras promulgated a cosmology that was largely of mythic and religious significance and that Philolaus, while maintaining some of this religious import, significantly reworked these ideas in order to produce a system that could account for basic astronomical phenomena (Huffman 2013). Graham has thus recently argued that Philolaus is not the mere transmitter of the earlier philosophy of Pythagoras but rather was the inventor of “Pythagorean” philosophy, the figure who brought Pythagoreanism out of the shadowy world of Pythagorean lore into the light of Greek philosophical conversation (Graham 2014: 48).
7.2 Philolaus and Plato
There is the possibility that on his first visit to Southern Italy and Sicily in 388–7 Plato met an aged Philolaus in Tarentum (D. L. III 36). This would motivate Plato’s allusion to Philolaus as the teacher of Socrates’ interlocutors, Simmias and Cebes, in the Phaedo, which scholars have often dated in the years immediately following Plato’s return from Italy. The presentation of Philolaus in the Phaedo is not particularly favorable; Socrates supposes that Cebes should have heard something from Philolaus about the prohibition on suicide, but Cebes responds that he has heard nothing clear on the topic from Philolaus, or anyone else. Plato may also be criticizing Philolaus when he shows the inconsistency between the doctrine that the soul is a harmony and the belief that the soul is immortal (see 6.2 above). On the other hand, late in Plato’s life, in the Philebus, there is evidence that Plato had studied Philolaus’ metaphysical system and derived fruitful insights from it. At 16b4 ff. Socrates introduces a philosophical method which he describes as
a gift … hurled down from the gods to man along with a dazzling fire on account of some Prometheus. And the men before our time, since they were better than we are and lived closer to the gods, handed down this report about the things that are in each case said to be, that they are from a one and many and that they have limit and unlimited in themselves by nature.
There are a number of important correspondences between the description of the method of “the men before our time” in this and the immediately following passages of the Philebus and the fragments of Philolaus, e.g., the postulation of the limit and unlimited as basic principles, Plato’s insistence that number is the basis for all inquiring, learning, and teaching (16e; Philolaus, Fr. 4) and the use of the musical scale as a central example of the combination of limiter and unlimited (17b ff., Philolaus, Fr. 6a). There can be little doubt that Plato has Philolaus in mind, and he may be alluding to Philolaus’ method of archai (Huffman 2001). It is clear, however, that Plato is not taking over Philolaus’ metaphysical system wholesale but is rather using it as a way of addressing problems that have arisen with the theory of forms. Meinwald (2002) argues that Plato is either correcting or providing a sympathetic reinterpretation of Philolaus’ system, which allows Plato to suggest a way in which knowledge of forms may be mathematical. This reinterpretation transforms unlimiteds into pairs of opposites, in which limiters set ratios. This interpretation agrees with Aristotle’s claim that Plato differed from the Pythagoreans in making the unlimited a dyad (Metaph. 987b23–27). It has been common to assume that the Prometheus in the passage quoted above is a veiled reference to Pythagoras (Hackforth 1958, 21; Gosling 1975, 83). Yet, as we have seen, Aristotle never associates Pythagoras with this metaphysical scheme, and Plato elsewhere presents Pythagoras as a founder of a way of life and not as a master metaphysician (R. 600a–b). Modern scholars may be overreading the passage in light of Pythagoras’ fame in the later tradition. Prometheus was traditionally the founder of all human arts through his gift of fire, and Plato here supposes that the philosophical method he describes must likewise have been due to some Prometheus, perhaps under the influence of Philolaus’ own allusion to Prometheus in his cosmology (see 4.2 above). There is no need to introduce Pythagoras into the story (Huffman 1999). Philolaus’ metaphysics of limiters and unlimiteds is perfectly intelligible as a response to the problems raised in the tradition of Presocratic metaphysics (see 2.1 above) and was not a gift either of Prometheus or Pythagoras. Some have argued that other passages in the Phaedo (101b10–104c9) and a passage in the Cratylus (401b11–c7) show that Plato was both heavily influenced by and critical of Philolaus (Horky 2013). However, neither Philolaus nor the Pythagoreans are specifically mentioned in these passages and the supposed connections to Philolaus are nothing like as specific as in the Philebus and too general and indirect to be convincing (e.g., the concepts of odd and even in the Phaedo passage were important to Philolaus but hardly limited to him).
Bibliography
Texts and Commentaries
- Diels, H. and W. Kranz, 1952, Die Fragmente der Vorsokratiker (in three volumes), 6th edition, Dublin and Zürich: Weidmann, Volume 1, Chapter 47, pp. 421–439. (Greek texts of the fragments and testimonia with translations in German. Referred to as DK.)
- Huffman, C. A., 1993, Philolaus of Croton: Pythagorean and Presocratic, Cambridge: Cambridge University Press. (Greek texts of the fragments and testimonia with translations and commentary in English.)
- Timpanaro Cardini, M., 1958–64, Pitagorici, Testimonianze e frammenti, 3 vols., Firenze: La Nuova Italia, Vol. 2, 262–385. (Greek texts of the fragments and testimonia with translations and commentary in Italian.)
General Bibliography
- Anatolius, 1901, Sur les dix premiers nombres, J. L. Heiberg (ed.), Paris: Libraire Colin.
- Aristotle, 1984, Fragments, in The Complete Works of Aristotle (Volume 2), Jonathan Barnes (ed.), Princeton: Princeton University Press, 2384–2465.
- Barker, A., 2007, The Science of Harmonics in Classical Greece, Cambridge: Cambridge University Press.
- Barnes, J., 1982, The Presocratic Philosophers, London: Routledge.
- Betegh, G., 2014, ‘Pythagoreans, Orphism and Greek Religion,’ in Huffman 2014: 149–166.
- Brisson, L., 2007, ‘Aristoxenus: His Evidence on Pythagoras and the Pythagoreans. The Case of Philolaus,’ in Die Griechische Biographie in Hellenistischer Zeit, Michael Erler and Stefan Schorn (eds.), Berlin: De Gruyter 269–283.
- Burch, G. B., 1954, ‘The Counter-Earth,’Osiris, 11: 267–294.
- Burkert, W., 1961, ‘Hellenistische Pseudopythagorica,’ Philologus, 105: 16–43, 226–246.
- –––, 1972a, Lore and Science in Ancient Pythagoreanism, E. Minar (trans.), Cambridge, Mass.: Harvard University Press, 1st German edition, 1962.
- –––, 1972b, ‘Zur geistesgeschichtlichen Einordnung einiger Pseudopythagorica,’ in Pseudepigrapha I, Fondation Hardt Entretiens XVIII, Vandoeuvres-Genève, 25–55.
- Bywater, I., 1868, ‘On the Fragments Attributed to Philolaus the Pythagorean,’ Journal of Philology, 1: 20–53.
- Centrone, Bruno, 1990, Pseudopythagorica Ethica, Naples: Bibliopolis.
- –––, 2014, ‘The pseudo-Pythagorean Wrtings,’ in Huffman 2014: 315–40.
- Creese, D., 2010, The Monochord in Ancient Greek Harmonic Science, Cambridge: Cambridge University Press.
- Dicks, D. R., 1970, Early Greek Astronomy to Aristotle, Ithaca: Cornell University Press.
- Diogenes Laertius, 1925, Lives of Eminent Philosophers, R. D. Hicks (tr.), Cambridge, Mass.: Harvard University Press. (Referred to as D. L.)
- Furley, D., 1987, The Greek Cosmologists, Cambridge: Cambridge University Press.
- Gosling, J. C. B., 1975, Plato: Philebus, Oxford: Clarendon Press.
- Gourevitch, D., 1989, ‘L’Anonyme de Londres et la médecine d’Italie du Sud,’ History and Philosophy of the Life Sciences, 11: 237–51.
- Graham, D. W., 2014, ‘Philolaus,’in Huffman 2014: 46–68.
- –––, 2015, ‘On Philolaus’ astronomy,’ Archive for History of Exact Sciences, 69(2): 217–30.
- Guthrie, W. K. C., 1962, A History of Greek Philosophy (Volume 1), Cambridge: Cambridge University Press.
- Hackforth, R., 1958, Plato’s Examination of Pleasure, Cambridge: Cambridge University Press.
- Hagel, S., 2009, Ancient Greek Music: A New Technical History, Cambridge: Cambridge University Press.
- Horky, P. S., 2013, Plato and Pythagoreanism, Oxford: Oxford University Press.
- Huffman, C. A., 1988, ‘The Role of Number in Philolaus’ Philosophy,’ Phronesis, 33: 1–30.
- –––, 1999, ‘Limite et illimité chez les premiers philosophes grecs,’ in La Fêlure du Plaisir : Études sur le Philèbe de Platon, Vol. II: Contextes, M. Dixsaut (ed.), Paris: Vrin, 11–31.
- –––, 2001, ‘The Philolaic Method: The Pythagoreanism behind the Philebus,’ in Essays in Ancient Greek Philosophy VI: Before Plato, A. Preus (ed.), Albany: State University of New York Press, 67–85.
- –––, 2007, ‘Philolaus and the Central Fire,’ in Reading Ancient Texts, Volume I: Presocratics and Plato, Essays in Honour of Denis O’Brien, Suzanne Stern-Gillet and Kevin Corrigan (eds.), Leiden: Brill, 57–94.
- –––, 2008, ‘Another Incarnation of Pythagoras,’ Ancient Philosophy, 28: 201–225 (a review of Riedweg 2005).
- –––, 2009, ‘The Pythagorean Conception of the Soul,’in Body and Soul in Ancient Philosophy, Dorothea Frede and Burkhard Reis (eds.), Berlin: De Gruyter, 21–43.
- –––, 2012, ‘Commentary on McKirahan,’ Proceedings of the Boston Area Colloquium in Ancient Philosophy, 27: 233–238.
- –––, 2013a, ‘Reason and Myth in Early Pythagorean Cosmology,’ in Early Greek Philosophy: The Presocratics and the Emergence of Reason, Joe McCoy (ed.), Washington, D. C.: The Catholic University of America Press, 55–76.
- –––, 2013b, ‘Philolaus’ Critique of Heraclitus,’ in Doctrine and Doxography, David Sider and Dirk Obbink (eds.), Berlin: de Gruyter, 121–144.
- –––, 2014, A History of Pythagoreanism, Cambridge: Cambridge University Press.
- Iamblichus, 1991, On the Pythagorean Way of Life, John Dillon and Jackson Hershbell (trs.), Atlanta: Scholars Press. (Referred to as VP.)
- Kahn, C., 1993, ‘Pythagorean Philosophy before Plato,’ in The Pre-Socratics, Alexander P. D. Mourelatos (ed.), Princeton: Princeton University Press, 161–185.
- –––, 2001, Pythagoras and the Pythagoreans, Indianapolis: Hackett.
- Kirk, G. S., Raven, J. E., and Schofield, M., 1983, The Presocratic Philosophers, 2nd edition, Cambridge: Cambridge University Press.
- Kingsley, Peter, 1995, Ancient Philosophy, Mystery and Magic, Oxford: Clarendon Press.
- Laks, A. and Most, G., 2016, ‘Philolaus,’ in Early Greek Philosophy: Western Greek Thinkers (Part 1), A. Laks and G. Most (eds.), Cambridge, Mass: Harvard University Press (Loeb Classical Library), 145–185.
- Leitao, D. D., 2012, The Pregnant Male as Myth and Metaphor in Classical Greek Literature, Cambridge: Cambridge University Press.
- Lloyd, G. E. R., 1963, ‘Who is attacked in On Ancient Medicine?,’ Phronesis, 8: 108–26.
- Manetti, D., 1990, ‘Doxographical Deformation of Medical Tradition in the Report of the Anonymus Londinensis on Philolaus,’ Zeitschrift für Papyrologie und Epigraphik, 83: 219–33.
- Mansfeld, J., 2010a, ‘Physikai Doxai and Problemata Physika in Philosophy and Rhetoric: From Aristotle to Aëtius (and Beyond)’ in Mansfeld and Runia (2010) 33–97.
- –––, 2010b, ‘Physical doxai in the Phaedo,’ in Mansfeld and Runia (2010) 183–201.
- –––, 2016, ‘Das verteufelte Lastschiff: Philolaus fr. 44.B12 DK,’ Mnemosyne, 69: 298–9.
- Mansfeld, J. and D. T. Runia, 2010, Aëtiana: The Method and Intellectual Context of a Doxographer. Volume Three: Studies in the Doxographical Traditions of Ancient Philosophy, Leiden: Brill.
- McKirahan, R., 2012, ‘Philolaus on Number,’ Proceedings of the Boston Area Colloquium in Ancient Philosophy, 27: 211–232.
- –––, 2016, ‘Philolaus on the Soul,’ in Renger and Stavru 2016: 63–76.
- Meinwald, Constance Chu, 2002, ‘Plato’s Pythagoreanism,’ Ancient Philosophy, 22(1): 87–101.
- Minar, E., 1942, Early Pythagorean Politics, Baltimore: Waverly Press.
- Moraux, P., 1984, Der Aristotelismus bei den Griechen von Andronikos bis Alexander von Aphrodisias, Zweiter Band: Der Aristotelismus im I. und II. Jh. n. Chr., Berlin: Walter De Gruyter.
- Mourelatos, A. P. D., 2006, ‘The Concept of the Universal in Some Later Pre-Platonic Cosmologists,’ in A Companion to Ancient Philosophy, Mary Louise Gill and Pierre Pellegrin (eds.), Oxford: Blackwell, 56–76.
- Mueller, I., 1997, ‘Greek arithmetic, geometry and harmonics: Thales to Plato,’ in Routledge History of Philosophy Vol. I: From the Beginning to Plato, C. C. W. Taylor (ed.), London: Routledge, 271–322.
- Netz, R., 2005, ‘The Pythagoreans,’in Mathematics and the Divine: A Historical Study, T. Koetsier and L. Bergmans (eds.), Amsterdam: Elsevier, 77–97.
- Nussbaum, Martha, 1979, ‘Eleatic Conventionalism and Philolaus on the Conditions of Thought,’ Harvard Studies in Classical Philology, 83: 63–108.
- O’Meara, D. J., 1989, Pythagoras Revived. Mathematics and Philosophy in Late Antiquity, Oxford: Clarendon Press.
- Palmer, J., 2018, ‘Presocratic Interest in the Soul’s Persistence after Death,’ in Philosophy of Mind in Antiquity: The History of the Philosophy of Mind (Volume 1), J. E. Sisko (ed.), New York: Routledge, 23–43.
- Philip, J. A., 1966, Pythagoras and Early Pythagoreanism, Toronto: University of Toronto Press.
- Primavesi, O., 2014, ‘Aristotle on the “so-called Pythagoreans”: from lore to principles,’ in Huffman 2014: 227–249.
- Renger, A-B. and Stavru, A., 2016, Pythagorean Knowledge from the Ancient to the Modern World: Askesis, Religion, Science, Wiesbaden: Harrassowitz.
- Ricciardetto, A. (ed.), 2016, L’Anonyme de Londres, Paris: Les Belles Lettres.
- Riedweg, Christoph, 2005, Pythagoras: His Life, Teaching, and Influence, Ithaca and London: Cornell University Press.
- Schibli, H. S., 1996, ‘On “The One” in Philolaus, Fragment 7,’ The Classical Quarterly (New Series), 46(1): 114–130.
- Sedley, David, 1995, ‘The Dramatis Personae of Plato’s Phaedo,’ in Philosophical Dialogues: Plato, Hume, Wittgenstein, T. J. Smiley (ed.), Oxford: Oxford University Press, 3–26.
- Stamatellos, G., 2007, Plotinus and the Presocratics, Albany: State Universty of New York Press.
- Thesleff, H., 1961, An Introduction to the Pythagorean Writings of the Hellenistic Period, Åbo: Åbo Akademi.
- –––, 1965, The Pythagorean Texts of the Hellenistic Period, Åbo: Åbo Akademi.
- –––, 1972, ‘On the Problem of the Doric Pseudo-Pythagorica. An Alternative Theory of Date and Purpose,’ Pseudepigrapha I, Fondation Hardt Entretiens XVIII, Vandoeuvres-Genève, 59–87.
- West, M. L., 1971, Early Greek Philosophy and the Orient, Oxford: Oxford University Press.
- Zhmud, L., 1989, ‘“All is number?,”’ Phronesis, 34: 270–92.
- –––, 1997, Wissenschaft, Philosophie und Religion im frühen Pythagoreismus, Berlin: Akademie Verlag.
- –––, 1998, ‘Some Notes on Philolaus and the Pythagoreans,’ Hyperboreus, 4: 1–17.
- –––, 2012, Pythagoras and the Early Pythagoreans, Oxford: Oxford University Press.
- –––, 2016, ‘Greek Arithmology: Pythagoras or Plato?,’ in Renger and Stavru 2016: 321–26.
- –––, 2018, ‘Physis in the Pythagorean Tradition,’ Philologia Classica, 13(1): 50–68.
Academic Tools
How to cite this entry. Preview the PDF version of this entry at the Friends of the SEP Society. Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers, with links to its database.
Other Internet Resources
[Please contact the author with suggestions.]


