Structured Propositions
It is a truism that two speakers can say the same thing by uttering different sentences, whether in the same or different languages. For example, when a German speaker utters the sentence ‘Schnee ist weiss’ and an English speaker utters the sentence ‘Snow is white’, they have said the same thing by uttering the sentences they did. Proponents of propositions hold that, speaking strictly, when speakers say the same thing by means of different declarative sentences, there is some (non-linguistic) thing, a proposition, that each has said.[1] This proposition is said to be expressed by both of the sentences uttered (taken in the contexts of utterance—to accommodate contextually sensitive expressions) by the speakers, and can be thought of as the information content of the sentences (taken in those contexts). The proposition is taken to be the thing that is in the first instance true or false. A declarative sentence is true or false derivatively, in virtue of expressing (in the context in which it is uttered—this contextual sensitivity shall henceforth be ignored and so qualifications of this sort dispensed with) a true or false proposition.
Propositions are thought to perform a number of other functions in addition to being the bearers of truth and falsity and the things expressed by declarative sentences. When a German and English speaker believe the same thing, say that the earth is round, the thing they both believe is not a sentence but a proposition. For the English speaker would express her belief by means of the sentence ‘The earth is round’ and the German speaker would express her belief by means of the different sentence ‘Die Erde ist rund’. Thus when people believe, doubt and know things, it is propositions that they bear these cognitive relations to. Finally, it is the proposition a sentence expresses, and not the sentence itself, that possesses modal properties such as being necessary, possible or contingent.
That propositions perform these various functions is agreed upon by virtually all advocates of propositions.[2] There is considerably less agreement concerning the nature of the things, propositions, that perform these functions.[3]
To say that propositions are structured is to say something about the nature of propositions. Roughly, to say that propositions are structured is to say that they are complex entities, entities having parts or constituents, where the constituents are bound together in a certain way. Thus, particular accounts of structured propositions can (and do) differ in at least two ways: 1) they can differ as to what sorts of things are the constituents of structured propositions; and 2) they can differ as to what binds these constituents together in a proposition. Various accounts of structured propositions that differ in these ways will be discussed below.
Put this way, the view that propositions are structured is purely a metaphysical thesis about what propositions are like and entails nothing about the relation between a sentence and the proposition it expresses. But of course structured proposition theorists do have views about the relation between a sentence and the proposition it expresses.
- 1. Setting Up the Problems
- 2. From Possible Worlds to Structured Propositions
- 3. Some Recent Accounts of Structured Propositions
- 4. Historical Antecedents to Current Views: Frege
- 5. Historical Antecedents to Current Views: Russell
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. Setting Up the Problems
Intuitively, given that a sentence expresses a structured proposition, the proposition will have parts or constituents that are the semantic values of words or subsentential complex linguistic expressions occurring in the sentence; and the proposition will have a structure similar to the structure of the sentence. For example, assuming that the semantic value of a name is its bearer and that the semantic value of a transitive verb is a relation, a structured proposition theorist will likely hold that the sentence
- (1) Jason loves Patty
expresses a proposition consisting of Jason, the loving relation and Patty, bound together in some way into a unity. Letting ‘j’ stand for Jason, ‘p’ for Patty and ‘L’ for the loving relation, we can represent the proposition in question as follows:
- (1a) [j[L[p]]]
Thus (1a)’s structure is very close to that of (1); and (1a) has as constituents the semantic values of the words occurring in (1). Indeed, in the case of (1) and (1a), all and only semantic values of words in the sentence are constituents of the proposition. But a given account of structured propositions may not hold that this is the case in general for any one of at least three reasons. First, one might hold that certain words as they occur in phrases in sentences do not contribute their semantic values to the propositions expressed by those sentences because the semantic values of these words instead partially determine the semantic values of the phrases in which they occur, where these latter semantic values are contributed to the proposition. For example, one might hold that in the sentence
- (2) Colin is a tall young man.
the phrase ‘is a tall young man’ contributes to the proposition expressed by (2) the property of being a tall young man, which is its semantic value. Thus, though the semantic value of the word ‘tall’ partly determines the semantic value of the phrase ‘is a tall young man’, the proposition expressed by (2) contains no constituent that is the semantic value of the word ‘tall’ alone. Second, one might hold that a sentence may express a proposition (in a context), where the proposition has constituents not contributed by any syntactic constituent of the sentence, let alone any word in the sentence. For example, Mark Crimmins [1992] claims that an utterance of the sentence
- (3) It’s raining
expresses a proposition to the effect that it is raining at a particular time and place. The present tense manages to somehow contribute the time of utterance to the proposition. But no syntactic constituent of the sentence contributes the place to the proposition, though Crimmins claims it is a constituent of the proposition expressed.[4] Third, one might hold that certain words simply have no semantic values, and so make no contribution to propositions. So-called neoplanastic ‘ne’ in French might be thought to be an example of this.
But even if, for one of the above reasons or some other reason, a sentence does not express a proposition whose constituents are precisely the semantic values of words in the sentence, we can still say that structured proposition theorists hold that sentences expresses propositions, where many (and likely most) constituents of the proposition are semantic values of words or phrases occurring in the sentence. So in the case of (1) and (1a), the constituents of the proposition are precisely the semantic values of the words in (1). In the case of (2) and (2a) (given the assumptions made above), the constituents of (2a) are precisely the semantic values of the name ‘Colin’ and the verb phrase ‘is a tall young man’. And in the case of (3), the proposition it expresses has three constituents, two of which are contributed by ‘raining’ and the present tense construction.
Thus, ignoring, or at least not dwelling on, the qualifications just made, we can say that structured proposition theorists hold that sentences express propositions that are complex entities (most of) whose constituents are the semantic values of expressions occurring in the sentence, where these constituents are bound together by some structure inducing bond that renders the structure of the proposition similar to the structure of the sentence expressing it.
This highlights an important feature of structured proposition accounts that distinguishes them from the other main competing account of propositions, namely the account of propositions as sets of possible worlds (to be discussed below). Because structured propositions have as parts the semantic values of expressions in the sentences expressing them, the semantic values of those expressions are recoverable from the semantic values of the sentences (i.e. the propositions).
It is perhaps worth noting that one could have a theory according to which the semantic values of expressions in a sentence are recoverable from the proposition expressed by the sentence, even though the semantic values of the expressions are not (mereological or set theoretic) parts of the proposition. For example, George Bealer [1993] formulates what he calls an algebraic conception of propositions (see also Bealer [1982]). Bealer associates with each proposition a “decomposition tree.” This decomposition tree shows how a given proposition is the result of the application of logical operations to individuals, properties, relations or other propositions (e.g. the application of the logical operation of negation to a proposition P yields a proposition that is true iff P is false; the application of the logical operation of singular predication to an item and a property yields a proposition that is true iff the item possesses the property, etc.). In general, a sentence will express a proposition such that the semantic values of expressions in the sentence will occur on the decomposition tree associated with the proposition. Thus, the semantic values of expressions in a sentence will be recoverable from the proposition (together with its decomposition tree) expressed by the sentence. However, Bealer denies that these semantic values are in any sense set-theoretic members or mereological parts of the proposition. Bealer appears to hold that the proposition is metaphysically simple and has no parts at all. As the term is used here then, Bealer’s is not an account of structured propositions for this reason. We will see below that others hold similar “algebraic” conceptions of propositions, where the propositions are complex entities consisting of constituents bound together in certain ways and so are structured propositions.
Since the structured proposition expressed by a sentence has a structure similar to that of the sentence and has as constituents semantic values of expressions occurring in the sentence, the theory of structured propositions allows for distinct necessarily equivalent propositions. For example, the propositions expressed by ‘Bachelors are unmarried’ and ‘Brothers are male siblings’ presumably are both necessarily true and hence are necessarily equivalent. But clearly the propositions expressed by these sentences have different constituents and so are distinct. The proposition expressed by the former presumably contains the semantic value of ‘bachelor’ (perhaps, the property of being a bachelor), whereas the proposition expressed by the latter doesn’t. And the proposition expressed by the latter contains the semantic value of ‘brother’, whereas the proposition expressed by the former doesn’t. This is an important virtue of the structured proposition view. The fact that it has this feature and that its main competitor, the possible worlds account of propositions (discussed below), doesn’t is one of the reasons many favor the structured proposition view.
In discussing recent accounts of structured propositions below, it will be shown how, on those accounts, sentences that are necessarily equivalent may express distinct propositions; and how the semantic values of expressions in a sentence are recoverable from the proposition expressed by the sentence.
2. From Possible Worlds to Structured Propositions
Because the structured proposition view arose in large part due to dissatisfaction with the then prevailing view of propositions, discussing this other account of propositions will help to illuminate structured proposition views. The late 1950s and 1960s saw the development of a new sort of model theory, “possible worlds semantics”, for systems of modal logic. In the framework of possible world semantics, linguistic expressions are assigned extensions “at” possible worlds. Thus, e.g. names, n-place predicates and sentences are assigned individuals, sets of n-tuples of individuals, and truth values, respectively, at different possible worlds. Intuitively, possible worlds are to be thought of as “ways things could have been”, and the assignment of (possibly different) extensions to expressions at different possible worlds is part of capturing this intuition. Thus there might have been more or fewer cows, and this is reflected in the fact that the extension of ‘cow’ (intuitively, the set of things that are cows) can vary from possible world to possible world.
Because we wish the extensions of expressions to vary from possible world to possible world (at least in some cases), it is natural to associate with each expression a function from possible worlds to extensions appropriate to that sort of expression. Thus we associate with names, functions from possible worlds to individuals; with n-place predicates functions from possible worlds to sets of n-tuples; and with sentences, functions from possible worlds to truth values. Such functions from possible worlds to extensions of the appropriate sort are often called intensions of the expressions in question, and the term ‘intension’ shall be used this way throughout the present work.[5] Now since most think that the extensions of sentences are truth values, as indicated above, the intension of a sentence is a function from possible worlds to truth values. Intuitively, it maps a world to true if the sentence is true at that world. Thus the intension of a sentence can be seen as the primary bearer of truth and falsity at a world: the sentence has the truth value it has at the world in virtue of its intension mapping that world to that truth value. Further, modal operators were typically construed as operating on the intensions of the sentences they embed, and so those intensions could plausibly be thought of as possessing modal properties. Since propositions were traditionally held to be the primary bearers of truth and falsity and the bearers of modal properties, it was natural for possible world semanticists to identify propositions with functions from possible worlds to truth values (sentential intensions), or equivalently, sets of possible worlds (the set of possible worlds at which the sentence in question is true). Indeed, this identification was thought by many to vindicate the previously mysterious notion of a proposition.[6] Possible worlds were apparently needed for the model theory of modal logic anyway; why not build propositions out of them?
Current structured proposition accounts arose largely out of dissatisfaction with the idea that propositions are sets of possible worlds (or functions from worlds to truth values). In fact, there were at least two quite distinct motivations for abandoning the view of propositions as sets of worlds and adopting the structured proposition account.
The first had to do with the way propositions are individuated on a possible worlds account. The view that propositions are sets of possible worlds does not individuate propositions very finely. For example, consider any pair of sentences that express metaphysically necessary propositions, say ‘Bachelors are unmarried’ and ‘Brothers are male siblings’. Since these propositions are true in all possible worlds, each must be the set of all possible worlds. But there is only one such set. Thus there is only one such proposition! Hence these two sentences express the same proposition. (The view also predicts that all true sentences of mathematics express the same (necessary) proposition, that any two necessarily equivalent sentences express the same proposition, that the conjunction of any sentence S with a necessarily true sentence expresses the same proposition as S, and so on.)
This should make clear that the account of propositions as sets of worlds is not a structured proposition account. For, as we saw, on a structured proposition account, the semantic values of expressions in a sentence are recoverable from the proposition expressed by the sentence, since those semantic values are constituents of the proposition. This is why on such an account, ‘Bachelors are unmarried males’ and ‘Brothers are male siblings’ express distinct propositions: the propositions have different constituents. But on the possible worlds account, the property of being a bachelor is in no sense recoverable from or a constituent of the proposition expressed by ‘Bachelors are unmarried’. For the latter proposition is just the set of all possible worlds. How could the property of being a bachelor be “recovered” from this set? Similarly, the property of being a brother is not recoverable from the proposition expressed by ‘Brothers are male siblings.’ Again, the latter proposition is just the set of all possible worlds.
Further, if propositions are sets of possible worlds, belief is construed as a relation between individuals and propositions and sentences of the form ‘A believes that P’ assert that the individual A stands in the belief relation to the proposition expressed by ‘P’, then for any necessarily equivalent sentences ‘P’ and ‘Q’, ‘A believes that P’ and ‘A believes that Q’ cannot differ in truth value. This means that, for example, if ‘A believes that 1+1=2’ is true, so is ‘A believes that there is no greatest natural number’. These consequences of the view that propositions are sets of possible worlds were appreciated early on; and theorists made a variety of attempts to make these consequences seem less unpalatable. Despite these valiant efforts, many philosophers viewed these consequences as a sign that there was something very wrong with the view that propositions are sets of possible worlds. Thus, philosophers were open to an account of propositions that individuated propositions more finely than the possible worlds account. As we have seen, the structured proposition account is just such an account.
In order to make clear the second motivation for abandoning the view of propositions as sets of worlds and adopting the structured proposition account, we must discuss the notions of rigid designation and direct reference. A rigid designator is an expression that designates the same individual in all possible circumstances or worlds. In the early 1970’s, Saul Kripke argued in Naming and Necessity that ordinary proper names are rigid designators. Kripke claimed that when we consider a sentence containing an ordinary proper name, such as
Aristotle was a great philosopher
and ask whether it would have been true or false in various counterfactual circumstances, it is the properties of the very same man, Aristotle, in those circumstances that are relevant to the truth of the sentence. So, ‘Aristotle’ designates the same man in these various counterfactual circumstances; it is a rigid designator.
At around the same time, David Kaplan argued that indexicals (e.g. ‘I’, ‘here’, ‘now’) and demonstratives (e.g. ‘that’, ‘you’, ‘he’) are directly referential. Concerning directly referential expressions, Kaplan wrote:
For me, the intuitive idea is not that of an expression which turns out to designate the same object in all possible circumstances, but an expression whose semantical rules provide directly that the referent in all possible circumstances is fixed to be the actual referent. In typical cases the semantical rules will do this only implicitly, by providing a way of determining the actual referent, and no way of determining any other propositional component. (Kaplan [1977] p. 493)
Thus, a directly referential expression is a rigid designator: its associated semantic rules determine the actual referent of the expression (in a context) and when evaluating what is said by the sentence containing the expression (in that context) in other possible circumstances, this same referent is always relevant. To illustrate, if John utters
I ski.
at the present time and we want to evaluate whether what John said by means of that utterance is true or false in other possible circumstances, it is John’s properties in those other circumstances that are relevant. Thus, ‘I’ is rigid: when evaluating the truth or falsity of what is said by an utterance of a sentence containing ‘I’ in counterfactual circumstances, it is the properties of the person whom ‘I’ referred to in the utterance (the actual utterer) that are relevant.
Kaplan intended to contrast directly referential expressions with expressions such as definite descriptions, which, though designating particular individuals, do so by means of descriptive conditions being expressed by the description and satisfied by the designated individual. Thus Kaplan wrote that directly referential expressions “refer directly without the mediation of Fregean Sinn as meaning”. (Kaplan [1977] p. 483) The designation of definite descriptions is mediated by something like a Fregean sense (i.e. their associated descriptive conditions).
Of course, even if descriptions are not directly referential, some are rigid designators. For example, ‘the successor of 1’ designates the same individual (2) in all possible worlds. So, though all directly referential expressions are rigid designators, some rigid designators are not directly referential. As was mentioned above, in a possible worlds semantics linguistic expressions are associated with intensions, functions from possible worlds to appropriate extensions. In the case of expressions designating individuals, these intensions will be functions from possible worlds to individuals. Note that all rigid designators (whether directly referential or not) will have intensions that are constant functions: they will be functions that map all possible worlds to the same individual. Thus possible worlds semantics tends to blur the distinction between directly referential expressions and rigid non-directly referential expressions (e.g. rigid definite descriptions). To make the distinction between directly referential expressions and rigid non-directly referential expressions more vivid, Kaplan invoked the notion of structured propositions:
If I may wax metaphysical in order to fix an image, let us think of the vehicles of evaluation—the what-is-said in a given context—as propositions. Don’t think of propositions as sets of possible worlds, but rather as structured entities looking something like the sentences which express them. For each occurrence of a singular term in a sentence there will be a corresponding constituent in the proposition expressed. The constituent of the proposition determines, for each circumstance of evaluation, the object relevant to evaluating the proposition in that circumstance. In general the constituent of the proposition will be some sort of complex, constructed from various attributes by logical composition. But in the case of a singular term which is directly referential, the constituent of the proposition is just the object itself. Thus it is that it does not just turn out that the constituent determines the same object in every circumstance, the constituent (corresponding to a rigid designator) just is the object. There is no determining to do at all. On this picture—and this is really a picture and not a theory—the definite description
- (1) The n[(snow is slight & n2=9) ∨ (~snow is slight & 22=n+1)]
would yield a constituent which is complex although it would determine the same object in all circumstances. Thus, (1), though a rigid designator, is not directly referential from this (metaphysical) point of view. (Kaplan [1977] p. 494–495)
(Kaplan goes on to attribute this “metaphysical picture” of structured propositions to Russell.) Adopting this structured proposition account makes it simple to distinguish between directly referential expressions and other expressions, rigid or not. Directly referential expressions contribute their referents (in a context) to the propositions expressed (in that context) by the sentences containing them. Non-directly referential expressions contribute some complex that may or may not determine the same individual in all possible circumstances. Thus the desire to distinguish clearly between directly referential expressions and other rigid designators prompted Kaplan to re-introduce the Russellian notion of a structured proposition into the philosophical literature (see the discussion of Russell below). However, Kaplan [1977] tends to treat the notion of a structured proposition as a heuristic device. He repeatedly calls it a picture, explicitly says that it is not part of his theory, and in his formal semantics he adopts the possible worlds account of propositions (contents of formulae), taking them to be functions from worlds (and times) to truth values.
Many current direct reference theorists take the structured proposition account much more seriously. It is part of their theory in the sense that when they say that an expression is directly referential they are literally saying that it contributes its referent to propositions expressed by sentences containing it, (e.g. see the discussion of Salmon and Soames below).
3. Some Recent Accounts of Structured Propositions
Having discussed structured proposition accounts in a general way, the best way to further illuminate these accounts of propositions is to discuss some recent work on structured propositions. In so doing, we shall see various respects in which accounts of structured propositions can differ. Three caveats before proceeding. First, as was mentioned above, structured proposition accounts, unlike possible world accounts of propositions, allow for distinct necessarily equivalent propositions, and thus individuate propositions more finely than possible worlds accounts. There are other accounts of propositions, or things that are intended to do the work of propositions, as in the previously mentioned example of Bealer [1993], that are not structured proposition accounts (given the way that term is used here), but that allow for distinct necessarily equivalent propositions or things that are to do the work of propositions. Another example is the interpreted logical form account defended by Larson and Ludlow [1993]. Though such accounts will not be discussed here, the reader should be aware of them and that they are motivated by many of the considerations that motivate structured proposition theorists. In particular, they attempt to individuate propositions (or things that do the work of propositions) more finely than possible worlds accounts of propositions. Second, discussing a sampling of recent work on the view that propositions are structured will not (and is not intended to) exhaust the versions of structured proposition approaches that there are. Rather, only some of the main issues and current approaches will be highlighted. To that end, three broad approaches to structured propositions will be discussed; these are the Neo-Russellian Approach, the Structured Intensions Approach, and the Algebraic Approach. In discussing each approach, a number of authors who adopt the approach will be mentioned, but for definiteness, only a representative of each approach will be highlighted in explaining it. The reader should be aware that these groupings are somewhat loose, and that there may be important differences among authors who are grouped together. Third, though questions will be raised here and there, criticisms of the various approaches discussed will be left aside. The task at hand is simply that of introducing the reader to approaches to structured propositions; criticizing the various approaches is a task for another day.
3.1 The Neo-Russellian Approach
In a series of papers and a book, Scott Soames [1985, 1987, 1989] and Nathan Salmon [1986a, 1986b, 1989a, 1989b] have laid out what is probably the best known current theory of structured propositions. There are some differences of detail between Salmon and Soames, but both shall be treated here as holding the same view. Though some of their contributions will be discussed separately, the main account followed will be that laid out in Soames [1987].
First, Soames [1985,1987] produced what many take to be a devastating attack on the view of propositions as sets of possible worlds. Soames showed that even when one tries to get more fine-grained propositions-as-sets-of-worlds by allowing metaphysically impossible worlds (e.g. worlds in which George Bush is identical with Ronald Reagan), inconsistent worlds (in which a thing can both possess and lack a property), and incomplete worlds (where some purported “matters of fact” are simply not settled), the resulting view, when combined with other independently plausible assumptions, is riddled with overwhelming difficulties. These difficulties all stem from the fact, noted earlier, that on the worlds view, sentences with very different syntactic structures and containing words with different semantic values may express the same proposition. Soames [1987] concludes that we ought to give up the view that propositions are sets of worlds of any sort, and embrace an account of propositions according to which propositions are structured entities, with individuals, properties and relations as constituents. Soames called these structured Russellian propositions. If the syntactic structures of sentences and the semantic values of words occurring in them are reflected in the structures and constituents of propositions they express, sentences with different syntactic structures and containing words with different semantic values, whether true in all the same worlds or not, may express different propositions. It is perhaps worth noting that having sentences with different syntactic structures and containing words with different semantic values express different propositions doesn’t require one to hold that propositions themselves are structured and contain the semantic values of the words as constituents. Still, it is a natural way of accounting for why sentences with different syntactic structures and containing words with different semantic values that are true in all the same worlds express different propositions. Soames [1987] sketches a formal theory of structured propositions, including an assignment of structured propositions to the sentences of a simple formal language, and a definition of truth relative to a circumstance for structured propositions.
Soames and Salmon are direct reference theorists, holding that names (as well as indexicals and demonstratives) have their referents as their semantic values and so contribute them to the propositions expressed by sentences containing them. Further they hold that predicates and intransitive verbs have properties as their semantic values; and that transitive verbs have relations as their semantic values. Thus they hold that sentences such as
- (4) Scott runs.
- (5) Scott saw Nathan.
express the propositions
- (4a) < < o >, R >
- (5a) < < o, o′ >, S >
where o is Scott , o′ is Nathan, R is the property of running, and S is the relation of seeing. The negation of (4) expresses the proposition
- (4b) < NEG, < < o >, R > >
where NEG is the truth function for negation. And the conjunction of (4) and (5) (in that order) expresses the proposition
- (5b) < CONJ< < < o >, R >, < < o, o′ >, S > > >
where CONJ is the truth function for conjunction. Similar remarks apply to sentences formed with other truth functional connectives. Further a sentence such as
- (6) Something runs.
expresses the proposition
- (6a) < SOME, g >
where SOME is the property of being a nonempty set and g is the function from individuals o′ to the proposition < < o′ >, R >, (where, as before, R is the property of running).
It should be easy to imagine the definition of truth relative to a circumstance for structured propositions of the sort mentioned above. For example, (5a) will be true at a circumstance c iff < o, o′ > is in the extension of the relation S at c. (5b) will be true at c iff CONJ maps the truth values of < < o >, R > and < < o, o′ >, S > at c to truth. And (6a) will be true at c iff there is an individual in c that g maps to a proposition that is true in c, (in that case the set of individuals in c that g maps to propositions true in c possesses SOME).
It should be clear that on this account of propositions sentences that are necessarily equivalent may express distinct propositions, and that the semantic values of expressions in a sentence are recoverable from the proposition it expresses. For example, ‘All bachelors are unmarried’ and ‘All brother are male’ are both true in all possible worlds. But on the present view, the former expresses a proposition that has as a constituent a propositional function mapping an object to the proposition that that object is unmarried; the latter does not. Further, e.g. the semantic value of ‘runs’ as it occurs in sentence (4) is recoverable from the proposition (4) expresses in that it is a constituent of that proposition. Similar remarks apply to 5/5a and 6/6a (except that in 6a the semantic value of ‘runs’ is encoded in g: that is, g maps individuals o to the proposition that o runs, which in turn has the semantic value of ‘runs’ as a constituent).
Note that this account of propositions (including the commitment to names being directly referential) entails that sentences that differ only with respect to coreferential names express the same proposition. Thus
Mark Twain is Samuel Clemens.
and
Samuel Clemens is Samuel Clemens.
express the same proposition on this view. Many have found this result incredible, since it would appear that the one sentence could be informative and the other not. Salmon and Soames also hold that ‘believes’ expresses a relation between individuals and propositions, so that ‘Scott believes that Mark Twain is Samuel Clemens’ expresses a proposition to the effect Scott stands in the believes relation to the proposition expressed by ‘Mark Twain is Samuel Clemens’. But then it follows that ‘Scott believes that Mark Twain is Samuel Clemens’ and ‘Scott believes that Samuel Clemens is Samuel Clemens’ express the same proposition (since the embedded sentences in both belief ascriptions express the same proposition) and so cannot diverge in truth value. Many have found this consequence of the Salmon-Soames view of propositions (and belief ascriptions) hard to swallow as well.
Salmon [1986] is largely an extended defense of these two consequences of the Salmon-Soames view. It is beyond the scope of the present work to explain Salmon’s defense and the interested reader should consult that work directly.[7] Soames [2002] deals with these issues, among others, as well.
In the formal semantics offered by Salmon and Soames, propositions are ordered n-tuples (or concatenations of n-tuples), as are (4a), (5a), (5b) etc. above. But since Salmon and Soames say nothing explicitly about the matter, it is unclear whether these n-tuples and concatenations merely represent propositions in the formalism, or whether Soames and Salmon take them to be propositions. If the former, then the Salmon and Soames view is incomplete and we need to be told what propositions really are, and more specifically what it is that really holds propositions together (i.e. what the corner brackets in (4a), (5a) etc. stand for). If the latter, then the view at least seems to have trouble accounting for some of the properties possessed by propositions. Propositions have truth conditions: they are true or false, depending on how the world is. So if some ordered n-tuples are propositions, some ordered n-tuples have truth conditions. But ordered n-tuples don’t seem to be the kinds of things that have truth conditions. Indeed, presumably many ordered n-tuples have no truth conditions, (e.g. < 1,2,3 >). So how/why did those n-tuples that are propositions come to have truth conditions? Similar remarks apply to modal properties. Propositions are necessary, contingent, and possible. These, again, don’t seem to be properties of n-tuples. Finally, if propositions are ordered n-tuples, that is, set theoretic constructions, it is hard to see why a particular set theoretic construction is the proposition in question (and so has truth conditions, modal properties, etc.) as opposed to some other set theoretic construction that seems equally well suited to the task. For example, we said that the sentence
- (4) Scott runs.
expresses the proposition/set theoretic construction
- (4a) < < o >, R >
But the following set theoretic construction seems equally suited to be the proposition (4) expresses:
- (4b) < R, < o > >
So why it is that (4a), instead of (4b), is the proposition (4) expresses, and has modal properties and truth conditions?
These questions as to what holds structured propositions together and gives them their structure, and how/why proposition have truth conditions turns us to other recent work within the neo-Russellian approach. While adopting more or less the same view as Salmon and Soames on the semantic values of different kind of words (though claiming to be strictly neutral on the question of what the semantic values of names and predicates are), Jeffrey C. King [1995, 1996, 2007, 2009] develops a view as to what binds the constituents of propositions together and how/why propositions have truth conditions. He holds that propositions are not n-tuples and that a complex relation binds together the constituents of a proposition and provides the proposition with its structure.[8] Further, King is motivated by the idea that propositions cannot be the kinds of things that by their very natures and independently of minds and languages have truth conditions. Hence, a radical feature of King’s view is that we speakers of natural languages endow propositions with their truth conditions, as a result of which he calls his account a naturalized account of propositions.
In order to explain what complex relation King claims binds the constituents together, consider the sentence ‘Dara swims’ and, idealizing considerably for the sake of exposition, assume that its syntactic structure at LF is as follows:
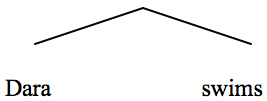
Figure 1.
Call the syntactic relation between ‘Dara’ and ‘swims’ here R. King sometimes calls R the sentential relation of the sentence ‘Dara swims’. Among the reasons that the English sentence in Figure 1 is true iff Dara swims is that the sentential relation R is interpreted by English speakers in a certain way. We interpret it as ascribing the semantic value of ‘swims’ to the semantic value of ‘Dara’. As King points out, this is a contingent matter. There might have been a language containing the sentence ‘Dara swims’ the speakers of which took the sentence to be true iff Dara fails to possess the property of swimming.[9] The difference in truth conditions of the sentence ‘Dara swims’ in these two languages is due to the speakers of the languages interpreting the syntactic concatenation in the sentence differently. And of course we English speakers interpreting R in the way we do (described above) is not an isolated matter. In general we interpret syntactic concatenation by composing semantic values of the concatenated lexical items in certain ways.[10] King sometimes puts this by saying that we interpret syntactic concatenation as instructing us to compose semantic values in certain ways. The fact that R in Figure 1 is interpreted by English speakers as ascribing the semantic value of ‘swims’ to the semantic value of ‘Dara’ is expressed by saying that in English, R encodes ascription.[11] It is the fact that R encodes ascription in English that makes the English sentence ‘Dara swims’ have truth conditions rather than being a list of Dara and the property of swimming.[12]
Returning to the main theme, we are trying to say what relation holds together Dara and the property of swimming in the proposition that Dara swims on King’s view. King claims that we ought to be sure that we pick a relation such that there are good independent grounds for thinking that Dara and the property really do stand in that relation, so that the proposition in question exists. Given that ‘Dara’ has Dara as its semantic value and that ‘swims’ has the property of swimming as its semantic value, then in virtue of the existence of the English sentence ‘Dara swims’, here is a two-place relation that Dara and the property of swimming stand in:
(Relation)
there is a language L, a context c and lexical items a and b of L
such that a and b occur at the left and right terminal nodes
(respectively) of the sentential relation R that in L encodes
ascription and ___ is the semantic value of a in c and ___ is the
semantic value of b in c.
Following King, let’s call an object possessing a property, or n objects standing in an n-place relation, or an object standing in a relation to a property, or n properties standing in an n-place relation and so on a fact. Then since Dara stands in the above relation to the property of swimming, the following is a fact:
(Fact)
there is a language L, a context c and lexical items a and b of L
such that a and b occur at the left and right terminal nodes
(respectively) of the sentential relation R that in L encodes
ascription and Dara is the semantic value of a in c and the property
of swimming is the semantic value of b in c.
That the English sentence ‘Dara swims’ exists, that ‘Dara’ has as its semantic value (in any context) Dara and that ‘swims’ has as its semantic value (in any context) the property of swimming jointly suffice for the existence of this fact. Equally, that the German sentence ‘Dara schwimmt’ exists (and that the words in the sentence have the semantic values in context that they do) and that the English sentence ‘I swim’ taken in a context in which Dara is the speaker exists each suffices for the existence of this fact as well. Without the existence of any such sentences, the fact in question wouldn’t exist.
(Fact), or what is the same thing, Dara standing in (Relation) to the property of swimming, is almost what King claims is the proposition that Dara swims. To see what more needs to be added, note that there is no reason to think that (Fact) has truth conditions and so is either true or false. But consider again (Relation), which relates Dara and the property of swimming in (Fact). Since Dara stands in (Relation) to the property of swimming in the proposition that Dara swims, call (Relation) the propositional relation of the proposition that Dara swims. Now if this propositional relation encoded ascription, as does the sentential relation R that is a component of the propositional relation, the proposition would have truth conditions. For in that case, the propositional relation would be interpreted as ascribing the property of swimming to Dara and so the proposition would be true iff Dara possesses the property of swimming.[13] Hence, King claims that the following fact is the proposition that Dara swims, where we now include as part of the fact/proposition that the propositional relation in it encodes ascription: there is a language L, a context c and lexical items a and b of L such that a and b occur at the left and right terminal nodes (respectively) of the sentential relation R that in L encodes ascription and Dara is the semantic value of a in c and the property of swimming is the semantic value of b in c.[14] Since Dara does possess the property of swimming, there is also the fact of her possessing this property. But note that this fact is quite distinct from the fact that King claims is the proposition that Dara swims. Still, the former makes the latter true. But had there been no fact of Dara possessing the property of swimming, the fact that is the proposition that Dara swims would still have existed and sadly would have been false.[15]
King claims that his account has several significant virtues.[16] First, on his account it is hard to deny that propositions exist given fairly minimal assumptions; and there is no mystery about what they are. Second, his theory is naturalized, in the sense that it is something we do that endows propositions with truth conditions. Third, and related to the previous point, we can give some explanation as to how and why propositions have truth conditions.[17] On the proposed explanation the representational powers of sentences and their users are explanatorily prior to those of propositions.
In more recent work, King has emended his account of propositions in various ways. On King’s [2007] view, because of the role the syntax of a sentence plays in the propositional relation expressed by the proposition it expresses, sentences with any difference in their syntactic structures express different proposition. However, in both King, Speaks, & Soames [2014] and especially in King [2018], King formulates a version of his view that allows sentences with quite different syntactic structures, whether in the same or different languages, to express the same proposition. In King, Speaks, & Soames [2014], King gives his most explicit account to date of how it is that propositions have truth conditions and so represent the world as being a certain way.[18]
Finally, we turn to a discussion of a view of propositions recently championed by Scott Soames [2010a, 2010b]. Soames follows King [2007, 2009] in rejecting the view that propositions are things that are representational, and so have truth conditions, independently of minds and languages on the grounds that such a view is ultimately mysterious and unintelligible. Again following King, Soames thinks that the fact that propositions are representational must ultimately be explained in terms of the representational capacities of agents. However, Soames’ positive account of how/why propositions have truth conditions differs in important ways from King’s.
Soames begins with the notion of the mental act of predication, which he takes to be primitive. However, by way of illustration, if an agent perceives an object o as red, and so has a perceptual experience that represents o as being red, the agent predicates redness of o. Similarly, if an agent “thinks of” o as red[19], or “form[s] the nonlinguistic perceptual belief that o is red”.[20] For Soames, predicating redness of o does not amount to believing that o is red. To believe that o is red, one must predicate redness of o and do something like endorse the predication. It is hard to say precisely what predicating amounts to since the notion is primitive for Soames. An agent predicating redness of o is an event token. Of course there may well be many event tokens of agents predicating redness of some object o by an agent perceiving it as red, an agent thinking of it as red and so on. Soames claims that the proposition that o is red is the event type of an agent predicating redness of o. Other more complex propositions are identified with events types of agents performing sequences of primitive mental acts.[21] Soames doesn’t say what he takes events (types or tokens) to be. But since he thinks that propositions are structured entities with constituents, he must think that event types are structured entities with constituents. Presumably, the proposition that o is red—the event type of an agent predicating redness of o—has o and redness as constituents.
Like King, Soames grounds the representational capacities of propositions in the representational capacities of agents. Soames claims that the event tokens of agents ascribing redness to o are things that inherently have truth conditions. They are things that are inherently true iff o is red. These tokens are for Soames tokens of the event type that is the proposition that o is red: the event type of an agent predicating redness of o. Soames claims that the event type that o is red has truth conditions because of its “intrinsic connection” to the event tokens of agents predicating redness of o, which, as indicated, are themselves things that inherently have truth conditions.
In King, Speaks, & Soames [2014] and Soames [forthcoming], Soames amends his theory of proposition in several respects. Two of those changes are the following. First, Soames [2010] had rejected the view that cognitive act types are propositions on the grounds that act type are things that we do, but propositions are not. In King, Speaks, & Soames [2014], Soames makes clear that he no longer finds this argument persuasive and is inclined to identify propositions with cognitive act types. Second, Soames gives a new account represent things as being a certain way. On the new account, propositions represent things as being a certain way in a derivative sense. Just as an act can be intelligent in the derivative sense that in performing it an agent is acting intelligently, the proposition that o is red represents in the derivative sense that in performing that act an agent represents o as being red.
Peter Hanks [2015] defends a view with some similarities to Soames’ view discussed above. As did Soames, Hanks follows King in endorsing the three novel claims from King [2007] and subsequent work mentioned above: (i) Hanks rejects theories according to which propositions have truth conditions and so represent the world as being a certain way by their very natures and independently of minds and languages as mysterious; (ii) holds that an adequate theory of propositions must explain how\why propositions have truth conditions and so represent the world as being a certain way; (iii) and holds that since the representational capacities of propositions cannot be something they have inherently and by their natures, their representational capacities must derive from and be explained by the representational capacities of thinking agents.
In simple cases of judging and asserting, Hanks claims we perform actions of predicating properties of objects. In judging that Donald Trump is a demagogue without speaking, one thinks of Trump (refers to him in thought), thinks of the property of being a demagogue (expresses the property in thought) and predicates the property of Trump. In asserting that Trump is a demagogue, one refers to him, expresses the property and predicates it of him, here using linguistic means. According to Hanks, in predicating a property of an object, one portrays the object as being a certain way and so does something that is true or false. Hence, Hanks claims these token acts of predicating are true or false. Hanks notion of predication is inherently assertive and committing, unlike Soames’ notion of predication. There is not some non-committal thing you do in predicating and then add endorsement or commitment. On Hanks view, predicating is committing to the object possessing the property in question. The proposition that Donald Trump is a demagogue is the act type of predicating being a demagogue of Trump. Hanks holds that this act type would exist even if it had no tokens. In general, whether they have tokens or not, Hanks holds that the act types that are propositions exist.
The proposition that Trump is a demagogue is the act type of referring to Trump, expressing the property of being a demagogue and predicating it of Trump, as we have seen. What Hanks calls the interrogative proposition expressible by the question ‘Is Trump a demagogue?’ is the act type of referring to Trump, expressing the property of being a demagogue and combining Trump and the property in an interrogative way (rather than predicating the property of Trump). Hanks gives a similar account of the imperative proposition expressed by the command ‘Trump, be a demagogue!’ As a result, Hanks rejects the claim that there is some common underlying content running through the (assertive) proposition, imperative proposition and interrogative proposition regarding Trump being a demagogue. There are just three different propositions here with their different “forces” (assertive, interrogative, imperative) built in.
Hanks’ explanation of why propositions as act types of the sort described have truth conditions comes in two steps. First, Hanks argues that token acts of predicating properties of objects have truth conditions. Hanks recognizes that some may doubt whether act tokens are the kinds of things that can be true and false. His main argument that they can be is that we have adverbial modifiers ‘truly’ and ‘falsely’ and that these attribute properties to action tokens. So just as ‘quickly’ in ‘Obama quickly stated that Clinton is eloquent.’ attributes a property to Obamas’s action, so Hanks claims that ‘truly’ in ‘Obama truly stated that Clinton is eloquent.’ attributes the property of being true to an action of Obama. Hanks then tries to argue that the action type of predicating being a demagogue of Cruz inherits the property of having truth conditions from its instances. Note that here it must be actual and possible instances that truth conditions are inherited from, since Hanks wants propositions that have never been and never will be tokened to have truth conditions. The argument here is complex since Hanks notes that types inherit certain kinds of properties from tokens and not others. Hence, Hanks seeks to explain why the having of truth conditions is the kind of property a type inherits from its (actual and possible) tokens.
On Hanks’ theory there are many more propositions than one might have thought. First, there is the proposition that is the act type consisting of referring to Clinton using ‘Clinton’ and predicating eloquence of her. It is true iff Clinton is eloquent. Then there is a distinct proposition with those same truth conditions that is the act of referring to Clinton in any way whatsoever and predicating eloquence of her. Next, there is another proposition with these same truth conditions consisting of the act of referring to Clinton using ‘Clinton’ while thinking of her as Obama’s former secretary of state and predicating eloquence of her. In addition, there is another proposition with the same truth conditions consisting of referring to Clinton using ‘Clinton’ while thinking of her as a former first lady and predicating eloquence of her. And so on. Again, all these propositions are true iff Clinton is eloquent. There is even a proposition consisting of referring to Clinton using ‘Clinton’ while drawing a round square and predicating eloquence of her. [22]
Above we saw that for Hanks, predication endows propositions with an inherent element of judgment or assertion. Predicating a property of an object commits the predicator to the object having that property. For Hanks, she did something false if it doesn’t. But this raises a problem for him. In disjunctive, negated, conditional propositions and others, embedded propositions do not have assertive force. They aren’t asserted. But if these embedded propositions inherently have an assertoric or judgmental element, how can this be? To address this Hanks claims that ‘or’, ‘if’ and ‘not’ create cancellation contexts. Since e.g. ‘or’ creates a cancellation context on Hanks’ view, in uttering the following sentence I fail to assert that Trump is a demagogue:
Trump is a demagogue or Clinton is eloquent.
Each disjunct expresses a proposition that includes as a sub act the act of predicating a property of the object according to Hanks. But the predication is cancelled. Hence, the asserting/committing element in the proposition is cancelled. Hanks must walk a very fine line here. The inherently assertive committal aspect of predication is what explains both that propositions are true and false and that unembedded propositions make assertions.[23] To explain why some embedded propositions don’t make assertions, Hanks appeals to the notion of the predication being cancelled in virtue of occurring in a cancellation context. But of course Hanks will want to say that the embedded proposition still has truth conditions and is true or false. Somehow in canceling the predication, though assertive force is cancelled the truth conditions and truth-value aren’t, even though predication is responsible for both.
Above it was mentioned that King [2007] and subsequent work endorsed three novel claims about propositions. Two of these are: (i) theories according to which propositions have truth conditions and so represent the world as being a certain way by their very natures and independently of minds and languages are mysterious and to be rejected; (ii) an adequate theory of propositions must explain how\why propositions have truth conditions and so represent the world as being a certain way.[24] It was also noted that Soames and Hanks follow King in this respect. In a sense, Speaks does too insofar as he feels the need to explain the “aboutness” or intentionality of some mental states.[25] So most recent literature has taken onboard King’s two claims above. Philosophy being what it is, however, there have been recent theorists who want to return to something like the classical theories of Frege and Russell, where propositions were thought to be mind and language independent abstract objects that by their very natures had truth conditions and so represent the world as being a certain way. On such a view, both of King’s claims are rejected. Propositions are precisely held to have truth conditions by their natures and independently of minds and languages; and it is denied that there can be any explanation of how/why propositions have truth conditions. Trenton Merricks [2015] defends such a view. According to Merricks, propositions are abstract, necessary existents that essentially represent the world as being a certain way.[26] He also holds that the fact that propositions essentially represent things as being a certain way is primitive. That is, this fact has no explanation.[27] Further, Merricks holds that propositions are simple: they have no constituents.[28] On this last point at least Merricks departs from the classical views of Frege and Russell on which propositions do have constituents.
Lorraine Juliano Keller [2014] expresses sympathy for a similar view that she calls propositional primitivism. On this view, propositions are fine-grained sui generis entities. They are not reducible to nor can they be explained by entities in another ontological category. Her primitivist thinks that not much of anything can be said about the inner nature of propositions except that they are abstract, mind and language independent entities with no constituents or structure. While King, Soames, Hanks and perhaps Speaks see in such a view mystery or worse, primitivists like Keller and Merricks see elegance and simplicity.
3.2 The Structured Intension Approach
Having seen the main features of neo-Russellian approaches, let us turn to structured meaning accounts. The roots of these accounts can be traced to Rudolf Carnap [1947], and his notion of intensional isomorphism. David Lewis [1972] and Max Cresswell [1985] have worked out similar, detailed versions of the structured meanings approach, though there are important differences in their views. Cresswell’s [1985] version of the view will be discussed here.[29] Because our concern is with conceptions of structured propositions, there are many features of Cresswell [1985] that will not be discussed (e.g. Cresswell’s account of the semantics of verbs of propositional attitude).
Both Lewis [1972] and Cresswell [1985] are motivated by some of the same considerations that motivated neo-Russellians like Salmon and Soames. Lewis and Cresswell both wish to find a more fine grained “semantic value” for sentences than functions from worlds (or, as in Lewis [1972], indices) to truth values or, equivalently, sets of worlds. For example, Cresswell [1985] claims that verbs of propositional attitude are (sometimes) sensitive to more than the intensions (functions from worlds/indices to truth values) of the sentences they embed. Thus Cresswell claims that
…one might easily have two sentences α and β that are true in exactly the same worlds and yet are such that
x φs that α
is true, but
x φs that β
is false. (Cresswell [1985] p. 73; φ of course is a verb of propositional attitude).
Thus Cresswell wishes to associate with a sentence (or more accurately, a ‘that’ clause) some semantic value that is more fine grained than a set of worlds, so that attitude verbs may (sometimes) distinguish between sentences that are true in exactly the same worlds. Strictly, Cresswell holds that sometimes attitude verbs are sensitive only to the sets of worlds in which the sentences they embed are true (i.e. their intensions); but sometimes attitude verbs are sensitive to more than this. In these latter cases, Cresswell wishes to associate a semantic value more fine grained than a set of worlds with the embedded sentence (or ‘that’ clause). Cresswell accomplishes this by holding that ‘that’ in English attaches to a sentence to form a name, and that ‘that’ in this role is highly ambiguous. In one of its meanings, ‘that’ attaches to a sentence and forms a name of the intension of the sentence (i.e. the set of worlds in which it is true).[30] In such cases, the attitude verb is sensitive only to the intension named by the ‘that’ clause following it. However, ‘that’ has another meaning on which it combines with a sentence to form the name of a much more fine-grained entity (in the sense that sentences true in all the same worlds may be associated with different fine-grained entities). In such cases, verbs of attitude are sensitive to differences in these fine-grained entities. Since our concern is with structured propositions, or with semantic values of sentences more fine grained than sets of worlds, the focus will henceforth be on Cresswell’s account of these fine-grained entities named by some ‘that’ clauses.[31] Henceforth, then, when the fine grained entity associated with a sentence or ‘that’ clause on Cresswell’s view is discussed, what is being discussed is what a ‘that’ clause containing the sentence names, given that the meaning of ‘that’ in the ‘that’ clause is the one that when combined with the sentence yields a name of the most fine grained entity named by any ‘that’ clause in which the sentence occurs. This is important to bear in mind, since for Cresswell, strictly speaking, a sentence not in a ‘that’ clause does not express this fine grained entity.
Consider the sentence
- (7) Max runs.
For Cresswell, the meaning of a predicate like ‘runs’ is essentially its intension: a function from individuals to sets of worlds (it maps an individual to the worlds at which she runs).[32] Let Ir be this intension. The meaning of a name like ‘Max’ (in some cases at least) is simply its referent: o. Thus, the fine grained entity associated with (7) is the ordered pair:
- (7a) < o, Ir >
The negation of (7) will be associated with the following:
- (7b) < NOT, < o, Ir > >
where NOT is the function from sets of worlds to sets of worlds that maps a set of worlds to its complement. Finally, the sentence:
- (8) Someone runs.
is associated with
- (8a) < Σ, Ir >
where Σ is the function from functions from individuals to sets of worlds to sets of worlds such that Σ(f)={w: for some o, w is in f(o)}.
It should be clear that as on the neo-Russellian approach, sentences that are true in all the same worlds may be associated with different fine grained entities of the sort posited by Cresswell. For example, even if ‘All brothers are siblings’ and ‘All bachelors are male’ are true in exactly the same worlds, the fine grained entity associated with the latter will contain the meaning (function from individuals to sets of worlds) of ‘male’ and the fine grained entity associated with the former will not. It should also be clear that the semantic values of expressions are recoverable from the propositions expressed by sentences containing them. For example, the semantic value of ‘runs’ as it occurs in (7) is a constituent of the fine-grained entity expressed by (7) (i.e. (7a)). Similar remarks apply to (7b) and (8a).
A final remark about Cresswell’s view is in order. The fine-grained entities we have been discussing are what verbs of propositional attitude are sensitive to when they are sensitive to more than the intension/set of worlds associated with a sentence they embed. However, they do not seem to be the primary bearers of truth for Cresswell. For Cresswell, each sentence is associated with a set of worlds/intension, which Cresswell calls a proposition; and the truth or falsity of a sentence at a world is determined by what proposition it expresses. So these seem to be the primary bearers of truth and falsity for Cresswell.[33] Thus, it appears that for Cresswell, in contrast to the neo-Russellians, the primary bearers of truth and falsity and the fine grained entities associated with the sentences (or ‘that’ clauses) that verbs of attitude embed and to which they are (sometimes) sensitive are different.
3.3 The Algebraic Approach
Finally, we turn to algebraic approaches. Though Bealer in some sense adopts an algebraic approach to propositions (see the above discussion), he apparently holds that propositions have no (set theoretic or mereological) parts, and so doesn’t count as a structured proposition theorist in the sense in which the term is used here. Thus, we will consider here adherents to the algebraic approach who do hold that the propositions yielded by their algebras are complex and have “parts”. Aside from Bealer [1979, 1982 and 1993], work in this tradition includes Edward Zalta [1983 and 1988], and Christopher Menzel [1993]. The focus here will be on the formulations in Edward Zalta [1988]. Though Zalta has an extensive, axiomatized theory of propositions, and ordinary and abstract individuals, properties, and relations, we confine our attention here to his view about propositions. Still, since Zalta views propositions as zero-place relations, we will say something about his views on properties and relations.
Advocates of the algebraic approach such as Zalta, like the neo-Russellians and the advocates of structured meaning approaches, think that a good theory of propositions must allow for distinct, necessarily equivalent propositions. Thus, he writes:
“Necessarily equivalent propositions may be distinct. If the theory of propositions is not fine-grained enough to distinguish necessarily equivalent propositions, the ability to accurately represent belief is lost” (Zalta 1988, p. 57)
To appreciate how Zalta achieves the goal of having a fine-grained theory of propositions, we begin by discussing how he views relations generally, since, as just mentioned, Zalta takes propositions to be zero-place relations (and properties to be one-place relations). Zalta holds that relations are “primitive entities”, by which he means that they are not to be explained or “defined” in terms of other entities/notions. But at least some relations are complex. For example, if we take a two-place relation (between objects) Rxy and “plug” one of its argument places with the object b, we get the one-place relation (property) Rxb (“bearing R to b”).[34] This one-place relation is complex, having b and R as parts. Similarly, if we take a three-place relation Sxyz and “universalize” the third argument position, we get a two place relation that we might represent thus: (z)Sxyz (“x and y (in that order) stand in S to everything”). Here again, the two-place relation is complex, having S and (something corresponding to) “universalization” as parts. Zalta’s idea is that properties, relations and individuals can be “harnessed together” to form new, complex relations. In his axiomatized theory of relations, Zalta introduces a comprehension schema for relations (see Zalta [1988] p. 46) that insures that all manner of complex relations will be available. To insure that all instances of the comprehension schema are true in all interpretations of his axiomatized theory, Zalta has these interpretations include the following group of “logical functions”: PLUGi, NEG, COND, UNIVi, REFLi, j CONVi, j, VACi, NEC, WAS and WILL. Roughly (and suppressing reference to worlds and times) PLUGi is a function that maps an n-place relation R and an object b to the n-1 place relation R′ such that < o1, …, oi-1, oi+1, …, on > stand in R′ iff < o1, …, oi-1, b, oi+1, …, on > stand in R. NEG is a function that maps an n-place relation R to an n-place relation R′ such that n things stand in R′ iff they don’t stand in R.[35] Thus the repeated application of these functions yields appropriate relations to make true the instances of Zalta’s comprehension schema for relations. For example, consider the following two instances of his comprehension schema (where ‘F′ is a variable ranging over one-place relations; ‘b’ is a name of an individual; and the other predicate letters are constants and so name particular relations):[36]
(∃F)(Fx iff Rxb)
(∃F)(Fx iff ~Px)
If we apply PLUG2 to the individual denoted by ‘b’ and the (two-place) relation denoted by ‘R’, we get a one-place relation that makes the first instance of the schema true; and if we apply NEG to the denotation of ‘P’, we get a one-place relation that makes the second instance true.
As we have mentioned, propositions are zero-place relations for Zalta. Thus, PLUGi and the rest of the “logical functions” mentioned above can be applied to various entities to yield propositions. Thus the proposition expressed by a sentence like
Ed runs.
is the result of applying the PLUG1 function to the property of running and Ed. This proposition consists of Ed saturating the one argument place of the running property. Similarly, a sentence like
Ed does not run.
expresses the proposition that is the result of applying PLUG1 to running and Ed as before, and then applying NEG to the output of PLUG1. Finally, a sentence like
Everything runs.
expresses the result of applying UNIV1 to the property of running. This idea that there is some group of “logical functions” whose repeated application to some other entities yield complex propositions (and relations) is characteristic of what are being called algebraic approaches.
It should be clear that necessarily equivalent sentences may express distinct propositions on Zalta’s view. For example, the sentences ‘All brother are male siblings’ and ‘All bachelors are unmarried’ express propositions that are true in all possible worlds. But the first expresses a proposition that results from applying COND to the properties of being a brother and being a male sibling, and applying REFL1,2 and then UNIV1 to the output of COND. The second does not, but instead results from applying these functions in the same order to the properties of being a bachelor and being unmarried. Further, it should be clear that the semantic values of expressions are recoverable from the propositions expressed by sentences in which they occur. E.g. both Ed and the property of running, which are the semantic values of ‘Ed’ and ‘runs’, are constituents of the proposition that Ed runs, which is expressed by ‘Ed runs’, since this proposition consists of Ed saturating the one argument place in the property of running.
Having sketched Zalta’s view of propositions it is worth mentioning a couple points about it. First, at least in some cases, what binds together the constituents of a proposition is in some sense “built into” one of the constituents of the proposition for Zalta, (as we shall see below, the same is true for Frege and Russell). Consider again the sentence:
Ed runs.
Recall that this sentence expresses the proposition that results from applying PLUG1 to Ed and the property of running. The output is Ed saturating (“plugged into”) the one argument place of the property of running. There are two things to notice about this proposal. First, it is one of the constituents of the proposition, the running property, that binds the constituents of the proposition together. The proposition is held together in virtue of Ed “plugging” the one argument place in the running property. Second, the proposition just is Ed “plugging”/possessing that property!
Such a view immediately raises a worry about false propositions (discussed below in connection with Russell’s POM account of propositions). For one might argue as follows. Suppose Ed doesn’t run. Then Ed doesn’t plug/saturate the one argument place in the property of running (i.e. doesn’t possess this property). But Ed possessing the running property just is the proposition that Ed runs. Thus there is no proposition that Ed runs. Similar reasoning shows that any other false proposition fails to exist. So there are no false propositions.
Obviously, Zalta does not want to be saddled with this result, and he isn’t. He holds that the even if Ed doesn’t run, there is a proposition consisting of Ed saturating the argument place in the running property. That proposition simply isn’t true. To put the point somewhat paradoxically, even if Ed doesn’t run, he possesses the property of running, so that we have our (false) proposition.
To some, Zalta will appear to have confused a proposition with what makes it true. Ed possessing the running property isn’t the proposition that Ed runs, one might think. It is what makes that proposition true! Of course Zalta must deny this. Having identified the proposition with the thing that other theorists take to be what makes the proposition true, Zalta holds that nothing outside of the proposition makes it true:
The metaphysical truth or falsity of these logical complexes [propositions] is basic. If a proposition is true, there is nothing else that “makes it true”. Its being true is just the way things are (arranged). (Zalta [1988] p.56)
So the idea is that whether Ed runs or not, he saturates the one argument place in the running property, so that we have the proposition that Ed runs. If Ed does run, so that the proposition is true, it is just a basic, brute fact that the proposition is true.
Finally, though we shall not go into it here, it is worth mentioning that when Zalta gets to the semantics of verbs of propositional attitudes, it is not only the propositions considered thus far that are objects of the attitudes and make belief ascriptions true or false. Zalta ends up claiming that sentences embedded with respect to attitude verbs are ambiguous, sometimes expressing the sorts of propositions we are discussing, and sometimes expressing other propositions that instead of containing the individuals, properties and relations thus far discussed, contain senses of these individuals, properties and relations. These senses are “abstract” individuals and relations, instead of the ordinary individuals and relations discussed thus far. Hence Zalta ends up with a theory of belief ascriptions that invokes both fine-grained propositions and neo-Fregean senses. The interested reader should consult Zalta [1988].
4. Historical Antecedents to Current Views: Frege
As with many ideas discussed in contemporary philosophy of language, the idea that propositions are structured is present in Gottlob Frege’s writings. Frege had a view both about the constituents of structured propositions and about what held these constituents together in the proposition. Frege held that simple linguistic expressions are associated with entities he called senses. Though there is some controversy about precisely how to understand the notion of sense, Frege explicitly distinguishes the sense of a linguistic expression from both the subjective ideas speakers associate with the expression and the thing in the world the expression “stands for”. Further, the sense of an expression determines what thing in the world the expression stands for. Thus the sense of a proper name such as ‘Ronald Reagan’ must be distinguished from any subjective ideas speakers associate with the name (e.g. feelings of anger, fondness, etc.) and from Reagan himself. And the sense of the name “picks out” Reagan as the thing in the world the name stands for. It may help to think of the sense as some descriptive condition satisfied uniquely by Reagan (and not to think any more about what is meant by a descriptive condition). Complex linguistic expressions are also associated with senses. And Frege held that the sense of a complex expression is a function of the senses of its simple parts and how they are put together. Frege called propositions thoughts (Gedanken), and held that the thought/proposition expressed by a sentence is itself a sense. And, like the senses of other complex linguistic expressions, the proposition/thought expressed by a sentence is a function of the senses of the words in the sentence and how they are put together. Now Frege at least sometimes appears to hold the stronger view that the sense of a sentence (proposition/thought) has as constituents the senses of the words in the sentence. And as the following quotation shows, his account of how these sense-constituents are held together in the proposition/thought depends on different kinds of linguistic expressions having different kinds of senses:
For not all parts of a thought can be complete; at least one must be ‘unsaturated’, or predicative; otherwise they would not hold together. For example, the sense of the phrase ‘the number 2’ does not hold together with that of the expression ‘the concept prime number ‘ without a link. We apply such a link in the sentence ‘the number 2 falls under the concept prime number’; it is contained in the words ‘falls under’, which need to be completed in two ways—by a subject and an accusative; and only because their sense is thus ‘unsaturated’ are they capable of serving as a link. (Frege [1892] p. 54)
Remarks like this suggest that Frege’s view was that propositions are complex entities whose parts are other senses. The proposition is held together in virtue of the fact that at least one of the senses is unsaturated (Frege sometimes also says predicative, or in need of supplementation). Other senses “saturate” or complete the unsaturated senses and in so doing are bound to them to form the proposition/thought. Thus, on this way of interpreting Frege, the mechanism for binding together the constituents of a structured proposition is built right into some of the constituents, (recall that this was true of the view of Zalta [1988] as well).
5. Historical Antecedents to Current Views: Russell
Bertrand Russell, to whom many current structured propositions theorists attribute the idea of structured propositions, held various views about the nature of propositions over the course of his career. However, the account of propositions held by Russell that is thought by many to be the progenitor of current accounts of structured propositions is the one Russell defended in Russell [1903]. We shall confine our attention to that account here. Russell differed with Frege both on what the constituents of structured propositions are and on what binds them together in the proposition. Russell uses the word ‘term’ for constituents of propositions. Thus he writes:
Whatever may be an object of thought, or may occur in any true or false proposition …I call a term….A man, a moment, a number, a class, a relation, a chimaera, or anything else that can be mentioned, is sure to be a term; and to deny that such and such a thing is a term must always be false. (Russell [1903] p. 43)
Thus we already see that Russell differs from Frege on what kinds of things can be constituents of propositions. For Frege, all constituents of propositions are senses. For Russell, a man or a mountain can be a constituent of a proposition. In a now famous correspondence with Frege, Russell replied to Frege’s assertion that the sense of the name ‘Mont Blanc’, and not Mont Blanc itself “with all its snowfields”, occurs in the proposition/thought that Mont Blanc is 4,000 meters high, by saying:
I believe that in spite of all its snowfields Mont Blanc itself is a component part of what is actually asserted in the proposition ‘Mont Blanc is more than 4,000 metres high’. (Frege [PMC] p. 169)
Russell goes on to distinguish two kinds of terms or propositional constituents:
Among terms, it is possible to distinguish two kinds, which I shall call respectively things and concepts. The former are the terms indicated by proper names, the latter those indicated by all other words. (Russell [1903] p. 44)
So for Russell, all propositional constituents are things or concepts. On Russell’s view, a sentence such as:
Socrates is human
expresses a proposition with three constituents, corresponding to the three words in the sentence. Socrates himself is one of the constituents, the other two constituents being the concepts contributed by ‘is’ and ‘human’.
Having seen that Russell held different kinds of things to be constituents of propositions than did Frege, we shall turn to his views on what binds together the constituents of structured propositions. Russell appears to hold that the propositional contributions of verbs (which contributions Russell often calls verbs) hold together the constituents of propositions. Thus he writes:
Consider, for example, the proposition ‘A differs from B’. The constituents of this proposition, if we analyze it, appear to be only A, difference, B. Yet these constituents, thus placed side by side, do not reconstitute the proposition. The difference which occurs in the proposition actually relates A and B, whereas the difference after analysis is a notion which has no connection with A and B. (Russell [1903] p. 49)
And later Russell writes:
Owing to the way in which the verb [propositional contribution of a verb] actually relates the terms of a proposition, every proposition has a unity which renders it distinct from the sum of its constituents. (Russell [1903] p. 52)
Russell’s idea that a proposition is something beyond the sum of its constituents certainly seems correct. The collection, or mereological sum, of A, difference and B is not the proposition that A differs from B. Different propositions may have the same Russellian constituents, as with the propositions expressed by the following sentence pair:
Jason loves Patti.
Patti loves Jason.
However, Russell’s idea that the propositional contribution of the verb binds the constituents together (in different ways in the case of our pair of sentences) is hard to understand. In the next to last quotation from Russell above, he suggests that the proposition expressed by ‘A differs from B’, whose constituents are A, difference and B, is held together by difference actually obtaining between A and B. If we call difference a relation, the proposition would consist of A standing in the relation of difference to B. Russell makes a number of remarks that suggest that this is his view. But it would seem that this cannot be correct. Intuitively, A standing in the relation of difference to B is what makes the proposition that A differs from B true. It is not the proposition itself. For if it were, it would seem that if A doesn’t stand in the difference relation to B, then there is no (false) proposition to the effect that A differs from B. And quite generally, for the same reason it would appear that there are no false propositions. Perhaps Russell meant that propositional contributions of verbs hold propositional constituents together in some other manner. But it certainly is not clear what that manner would be. Or perhaps he held a view similar to Zalta’s discussed above.
Bibliography
- Bealer, George, 1979, ‘Theories of Properties, Relations and Propositions’, Journal of Philosophy 76: 634–648.
- –––, 1982, Quality and Concept, Oxford: Clarendon Press.
- –––, 1993, ‘A Solution to Frege’s Puzzle’, in Philosophical Perspectives (Volume 7: Language and Logic), pp. 17–60, Atascadero, CA: Ridgeview Publishing Company.
- Carnap, Rudolf, 1947, Meaning and Necessity, Chicago: University of Chicago Press.
- Cresswell, M.J., 1985, Structured Meanings, Cambridge, MA: MIT Press.
- Crimmins, Mark, 1992, Talk About Beliefs, Cambridge, MA: MIT Press.
- Frege, Gottlob, 1892, ‘On Concept and Object’, in Translations from the Philosophical Writings of Gottlob Frege, Geach and Black (eds.), Oxford: Basil Blackwell, 1977, pp. 42–55.
- –––, [PMC], Philosophical and Mathematical Correspondence, ed. Gabriel, Hermes, Kambartek, Thiel and Veraart, Chicago: University of Chicago Press, 1980.
- Hanks, Peter, 2009, ‘Recent Work on Propositions’, Philosophy Compass, 4(3): 469–486
- –––, 2015, Propositional Content, Oxford: Oxford University Press.
- Kaplan, David, 1977, ‘Demonstratives’, Draft #2, in Themes From Kaplan, Almog, Wettstein, Perry (eds.), Oxford: Oxford University Press, 1989, pp. 481–564.
- Keller, Lorraine, 2014, ‘The Metaphysics of Propositional Constituency’, Canadian Journal of Philosophy, 43: 655–78
- King, Jeffrey C., 1995, ‘Structured Propositions and Complex Predicates’, Noûs, 29(4): 516–535
- –––, 1996, ‘Structured Propositions and Sentence Structure’, Journal of Philosophical Logic, 25: 495–521
- –––, 2007, The Nature and Structure of Content, Oxford: Oxford University Press.
- –––, 2009, ‘Questions of Unity’, The Proceedings of the Aristotelian Society, 109: 257–277.
- –––, 2018, ‘On Propositions and Fineness of Grain (Again!)’, Synthese, 196(4): 1343–1367.
- King, Jeffrey C., Jeff Speaks, and Scott Soames, 2014, New Thinking About Propositions, New York: Oxford University Press.
- Kripke, Saul, 1972, 1980, Naming and Necessity, Cambridge, MA: Harvard University Press.
- Larson, R and P. Ludlow, 1993, ‘Interpreted Logical Forms’, Synthese, 95: 305–356
- Lewis, David, 1972, ‘General Semantics’, in Semantics of Natural Language, Davidson and Harman (eds.), Dordrecht: D. Reidel, pp. 169–218.
- Menzel, Christopher, 1993, ‘The Proper Treatment of Predication in Fine-grained Intensional Logic’, in Philosophical Perspectives, 7, Language and Logic, pp. 61–87, Atascadero, CA: Ridgeview Publishing Company.
- Merricks, Trenton, 2015, Propositions, Oxford: Oxford University Press.
- Montague, Richard, 1960, ‘On the Nature of Certain Philosophical Entities’, The Monist, 53: 159–94
- –––, 1970, ‘Pragmatics and Intensional Logic’ in Formal Philosophy: Selected Papers of Richard Montague, New Haven: Yale University Press, 1974.
- Richard, Mark, 1982, ‘Tense, Propositions and Meanings’ Philosophical Studies, 41: 337–351.
- –––, 1990, Propositional Attitudes: An Essay on Thoughts and How We Ascribe Them, Cambridge: Cambridge University Press.
- Russell, Bertrand, 1903, Principles of Mathematics, second Edition, New York: Norton.
- Salmon, Nathan, 1986a, Frege’s Puzzle, Cambridge: MIT Press/Bradford Books.
- –––, 1986b, ‘Reflexivity’, Notre Dame Journal of Formal Logic, 27(3): 401–429.
- –––, 1989a, ‘Illogical Belief’, Philosophical Perspectives, 3, Philosophy of Mind and Action Theory, Atascadero, CA: Ridgeview Publishing Company, p. 243–285.
- –––, 1989b, ‘Tense and Singular Propositions’, in Themes From Kaplan, Almog, Wettstein, Perry (eds.), Oxford: Oxford University Press, 1989, pp. 391–392.
- Soames, Scott, 1985, ‘Lost Innocence’, Linguistics and Philosophy, 8: 59–71.
- –––, 1987, ‘Direct Reference, Propositional Attitudes and Semantic Content’, Philosophical Topics, 15: 47–87.
- –––, 1989, ‘Semantics and Semantic Competence’, Philosophical Perspectives, 3, Philosophy of Mind and Action Theory, Atascadero, CA: Ridgeview Publishing Company, pp. 575–596.
- –––, 2002, Beyond Rigidity, New York: Oxford University Press.
- –––, 2010, What is Meaning?, Princeton: Princeton University Press.
- –––, 2019, ‘Propositions’, in Chris Tillman (ed.), The Routledge Handbook of Propositions, London: Routledge.
- Stanley, Jason, 2000, ‘Context and Logical Form’, Linguistics and Philosophy, 23: 391–434.
- Zalta, Edward N., 1983, Abstract Objects: An Introduction to Axiomatic Metaphysics, Dordrecht: D. Reidel.
- –––, 1988, Intensional Logic and the Metaphysics of Intentionality, Cambridge, MA: MIT Press.
Academic Tools
How to cite this entry. Preview the PDF version of this entry at the Friends of the SEP Society. Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers, with links to its database.
Other Internet Resources
[Please contact the author with suggestions.]
Acknowledgments
Thanks go to Mark Brown for spotting a use/mention error in Section 2 and for identifying other typographical errors which have now been corrected. Thanks to Annie Papreck King for help with manuscript preparation.


